Offentlig-nøkkel kryptografi
Se for deg at person A har en hengelås og at han sender den til deg (i åpen tilstand), men beholder nøkkelen. Du kan dermed låse inn en hemmelighet ved hjelp av hengelåsen og sende den til A. Bare A kan låse opp igjen, siden bare A har den riktige nøkkelen.
Her ser vi på hvordan dette kan gjøres ved hjelp av tall i stedet for en hengelås.
I teksten om klassisk kryptografi skulle Anna og Bente utveksle krypterte meldinger. Forutsetningen var at de på forhånd hadde blitt enige om en hemmelig nøkkel. Noen ganger er dette svært upraktisk. Et eksempel: Du ønsker å bestille en bok fra en amerikansk nettbokhandel. De ønsker adresse og telefonnummer, og ofte kredittkortnummer. Siden du vet at andre kan lese meldinger som sendes via internett, ønsker du å kryptere meldingen som inneholder disse opplysningene. Det er ikke aktuelt å dra til USA for å utveksle nøkler med nettbokhandelen. Hvis nettstedet bruker såkalt offentlig-nøkkel kryptografi, kan dette unngås.
Prinsippet er som følger: Nettstedet A har et par av nøkler som hører sammen: En offentlig nøkkel P som alle som ønsker det kan få tak i, og en privat, hemmelig nøkkel S som bare nettstedet selv kjenner til.
Disse nøklene er laget slik at meldinger som krypteres med P kan bare dekrypteres med S. Altså, hvis du ønsker å sende en kryptert melding M til A, krypterer du den med P, og får den krypterte meldingen K, som du sender til A. Nå kan A ved hjelp av sin private nøkkel S, dekryptere K og dermed finne M. Alle andre, som også kan få tak i K, klarer ikke å dekryptere K, siden de ikke kjenner S.
Et system for offentlig-nøkkel kryptografi
Det finnes mange matematiske teknikker for å lage offentlig-nøkkel systemer. Den mest kjente og mest brukte er RSA, som du kan lese om i en annen tekst her. Et annet og enklere system vi kan bruke for å illustrere offentlig-nøkkel kryptografi, er basert på bruk av grafer. Vi anbefaler først å lese teksten om Grafer, algoritmer og effektivitet. Som nevnt i denne teksten er følgende et problem man ikke tror det er mulig å finne noen effektiv algoritme for å løse.
Noen viser deg en graf som har en perfekt kode. Kan du finne en perfekt kode?
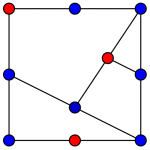
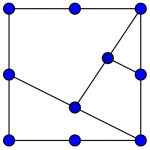
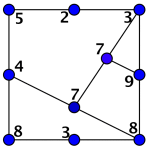
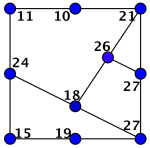
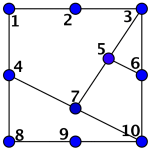
Figur 1: Eksempel på graf som har perfekt kode. Figur 2: Den offentlige nøkkelen. Figur 3: Et heltall i hvert hjørne slik at summen er 56 Figur 4: Kryptert melding.Tallet i hjørnet lagt sammen med tallene på nabohjørnene – fra figur 3. Figur 5: Nummerér hjørnene for å finne likningene.
En perfekt kode er altså en samling av hjørner (for eksempel de røde hjørnene i grafen under) i en graf slik at alle de andre hjørnene er nabo med nøyaktig ett rødt hjørne. I figur 1 er det et eksempel på en graf som har en perfekt kode (de røde hjørnene).
Vi skal lage et kryptosystem basert på dette: Den offentlige nøkkelen er en stor graf, mens den private (hemmelige) nøkkelen er en perfekt kode for grafen. Vi bruker grafen i eksemplet over, men nå uten at de røde hjørnene (den perfekte koden) er markert. Den offentlige nøkkelen ser altså ut som i figur 2.
Meldingene vi skal sende må være oversatt til heltall på en eller annen måte. Vi utsetter litt å se på hvordan dette kan gjøres. Meldingen 56 krypteres på følgende måte. Skriv et tall (heltall større enn 0) på hvert hjørne slik at summen av alle tallene er 56. I figur 3 er summen av alle tallene 56.
Deretter: For hvert hjørne i grafen, ta tallet som står på dette hjørnet og legg til tallene som står på alle nabohjørnene, se figur 4.
Disse tallene er den krypterte meldingen.
Hvordan dekryptere? Hvis du kjenner den perfekte koden er dette enkelt. Legg sammen tallene for alle hjørnene i den perfekte koden. Sjekk i eksemplet at dette virkelig blir 56. Ser du hvorfor det blir slik?
Hvordan knekke systemet?
Hvis du snapper opp det krypterte budskapet i figur 4, kan du sette opp 10 ligninger med 10 ukjente. De ukjente x1, x2, ..., x10 er tallene i figur 3. Ligningene finner vi ved å kikke på grafen. La oss nummerere hjørnene slik som i figur 5.
Siden hjørne 2 og hjørne 4 er naboer til hjørne 1, er den første ligningen
x1 + x2 + x4 = 11.
På høyresiden av likhetstegnet står det 11, siden dette er tallet som står på hjørne 1 i den krypterte meldingen. Slik får du en ny ligning for hvert hjørne. Siden naboene til hjørne 10 er hjørnene 6, 7 og 9, blir den siste ligningen
x6 + x7 + x9 + x10 = 27.
Nå er det slik at det finnes effektive måter å løse slike ligningssett på, også når de blir ganske store. En graf med 100 hjørner, ville gitt 100 ligninger med 100 ukjente. Dette er også løsbart, for en datamaskin med riktig programvare. Settet med 10 ligninger og 10 ukjente som over kan du kanskje løse for hånd? Dermed er ikke dette systemet sikkert i praksis. En matematiker og kjent kryptograf som heter Koblitz har foreslått en variant av dette systemet som kan være sikker.
Fra tekst til tall
Det er mange måter å oversette tekst til tall på. Du kan også lese om dette i teksten om det binære tallsystemet.
En veldig enkel metode er å erstatte hver bokstav med nummeret i alfabetet, altså la A erstattes med 1, B med 2 osv. En variant av dette (som ofte er nyttig) får du hvis du istedet starter å telle på 0, slik at A erstattes med 0 og B erstattes med 1 osv.
Hva om man ønsker litt større tall? Det finnes bokstavpar, altså AA, AB, AC,..., ÅÅ. En naturlig måte å nummerere dem fra 0 til 840 på er AA er 0, AB er 1, AÅ blir 28, mens BA blir 29, BB blir 30 osv. F. eks. blir LP par nummer siden L er bokstav nummer 11, og P nummer 15 (husk vi starter å telle på 0). Generelt, hvis den føreste bokstaven er bokstav nummer x og den andre bokstaven i paret er bokstav nummer y, blir nummeret til paret . La oss se på teksten TALL. Den består av to par: TA og LL. Siden T er bokstav nummer 19, og A bokstav nummer 0,blir TA oversatt til . Bokstaven L er nummer 11, slik at LL blir .
Del på Facebook