Grafer, algoritmer og effektivitet

Noen ting kan gjøres raskt, andre ting tar lengre tid. Slik er det også med matematiske beregninger. Det finnes en del problemer vi ikke vet om kan løses effektivt eller ikke, men som erfaringen tilsier at det sannsynligvis ikke finnes noen effektiv metode for å løse. La oss ta et eksempel som du kjenner godt. Finn to store primtall (dvs. tall som bare er delelig med seg selv og 1), f.eks. 67 og 83. På barneskolen lærer vi en metode (eller algoritme) for å regne ut produktet. Er vi godt øvet, gjør vi det for hånd. Er vi late, bruker vi kalkulatoren, som finner svaret veldig raskt.

Det motsatte problemet er å faktorisere tall. Får du oppgitt tallet 5561, vil det antagelig ta deg litt tid å finne ut hva faktorene er (svaret er at $5561=67\cdot 83$). Har du god tid, kan du prøve å faktorisere 655411.

La t være tallet du vil faktorisere. Hvordan skal du gå fram for å gjøre faktoriseringen mest mulig effektivt? Ingen vet svaret på dette spørsmålet. Det finnes mange algoritmer, men alle har den egenskapen at når man øker størrelsen på tallet t litt, så øker tiden det tar å faktorisere t mye. Ta to primtall p og q, begge med 100 sifre, og beregn n = pq. Da vil (i 2003) ingen datamaskin i hele verden klare å faktorisere n.

Legg merke til ordbruken vår her. Vi snakker om problemer, f.eks. å faktorisere tall på den ene siden, og metoder (algoritmer) for å løse problemer, på den annen. Her er en algoritme for å faktorisere tallet t: Prøv å dele på alle tall mindre enn t. Denne metoden er svært lite effektiv, litt raskere går det hvis du bare prøver å dele på alle primtall mindre enn t. Det finnes algoritmer som er langt mer effektive enn denne også.

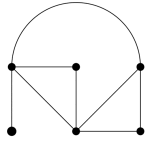
Figur 1: Eksempel på graf med 6 hjørner og 8 kanter.

For hver algoritme kan vi prøve å måle effektiviteten. I mange tilfeller vet vi ikke om det kan finnes andre algoritmer (som kanskje ingen har oppdaget ennå) som er enda bedre. Kanskje finnes en algoritme som faktoriserer et produkt av to primtall like effektivt som vår kjente metode multipliserer to tall. Ingen tror at en slik algoritme finnes, men vi vet det ikke sikkert! I kryptografi utnyttes, i RSA-systemet, at det ikke er kjent noen slik algoritme. Du kan lese om RSA-systemet i en annen tekst her.

Vi skal se på et par andre problemer som ingen kjent effektiv algoritme løser. Vi trenger da å ta en titt på grafer. Grafer er også diskutert i teksten om Broene i Königsberg. Vår definisjon er litt annerledes. En graf består av punkter (som kalles hjørner) og linjer mellom hjørnene (som kalles kanter). Det kan maksimalt være en kant mellom hvert par av hjørner. Figur 1 viser et eksempel på en graf med 6 hjørner og 8 kanter.

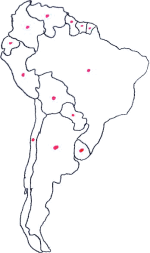
Figur 2: Kart over Sør-Amerika.

Fargelegging av kart og grafer

Kanskje kjenner du til følgende problem: Du har et kart, for eksempel over Sør-Amerika som i figur 2, og skal fargelegge landene slik at ingen land med felles grense får samme farge. Hvor mange farger trenger du?

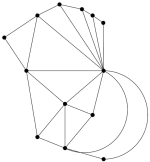
Vi sier at kartet er 3-fargeleggbart dersom tre farger er tilstrekkelig for en slik fargelegging, og at det er n-fargeleggbart dersom n farger er tilstrekkelig. Problemer er altså å finne den minste n slik at kartet er n-fargeleggbart. Generelt er dette ikke så enkelt som det kan høres ut til. Man kan erstatte kartet med en graf på følgende måte: Erstatt hvert land med et hjørne, og hver grense mellom to land med en kant mellom de to tilhørende hjørnene. Kartet over Sør-Amerika tilsvarer altså denne grafen, se figur 3.

Figur 3: Grafen til Sør-Amerika.

Slik kan du altså for hvert kart lage en graf, og problemet er nå: Hvor mange farger trenger du for å fargelegge hjørnene slik at to hjørner med en kant i mellom aldri har samme farge. Hvis grafen er stor er det et problem det kan ta svært lang tid å løse, siden ingen kjente effektive algoritmer finnes. Hvor mange farger trenges for Sør-Amerika? Svaret er fire, kan du overbevise deg om at tre ikke er nok?

Faktisk kan det vises at alle kart kan fargelegges ved hjelp av fire farger. Dette er et berømt problem, som ble løst for ikke så lenge siden. Man hadde lenge trodd at fire farger var tilstrekkelig, men beviset for dette kom først i 1976.

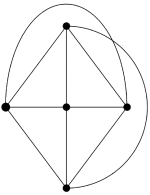
Selv om alle kart kan farvelegges med fire farger, finnes det grafer som ikke kan fargelegges med bare fire. Figur 4 viser et eksempel der du trenger fem farger (kan du se hvorfor?).

Figur 4: Graf som må fargelegges med 5 farger.

Dette motsier ikke det vi hevdet over, fordi denne grafen ikke tilsvarer noe kart. Denne grafen kan ikke tegnes uten at to kanter må krysse hverandre, mens alle kart gir opphav til en graf som kan tegnes uten at to kanter krysser hverandre! Grafer med denne egenskapen kalles planære. Et annet, nært beslektet problem: Noen gir deg en graf som er 3-fargeleggbar, og du skal finne en 3-fargelegging! Heller ikke her er det kjent noen effektiv algoritme.

Perfekte koder

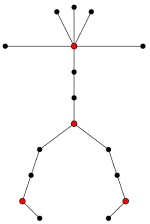
Figur 5: Graf med perfekt kode.

Et annet graf-problem hvor ingen effektiv algoritme er kjent er det såkalte perfekt kode-problemet. De røde hjørnene i grafen i figur 5 er et eksempel på en perfekt kode.

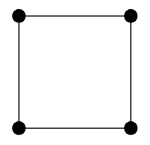
Det er nemlig slik at alle hjørnene enten er røde eller er nabo til nøyaktig ett rødt hjørne. Samlingen av røde hjørner kalles da en perfekt kode. Ikke alle grafer har perfekte koder. Figur 6 viser et enkelt eksempel på en som ikke har noen perfekt kode.

Figur 6: Graf uten perfekt kode.

Begge de følgende problem er av typen man ikke tror det kan finnes noen effektiv algoritme for å løse:

Avgjør om en (stor) graf har en perfekt kode eller ikke!

Noen viser deg en graf som har en perfekt kode, kan du finne en?

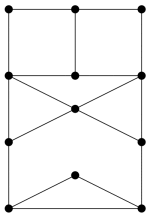
Prøv deg på følgende eksempel. Kan du finne en perfekt kode i grafen i figur 7?

Figur 7: Finnes det en perfekt kode?