Eksponential- og logaritmefunksjoner
Videoen forklarer sammenhengen mellom eksponential- og logaritmefunksjoner.
MatRIC: Eksponential- og logaritmefunksjoner
Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC
Begreper
GrafEn graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. |
KoordinatKoordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se Koordinatsystem |
Koordinatsystem
Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). Førsteakse
Den horisontale/vannrette aksen i et koordinatsystem. Kalles også for x-akse. |
Oppgaver
1. Regn ut og .
FASIT
og
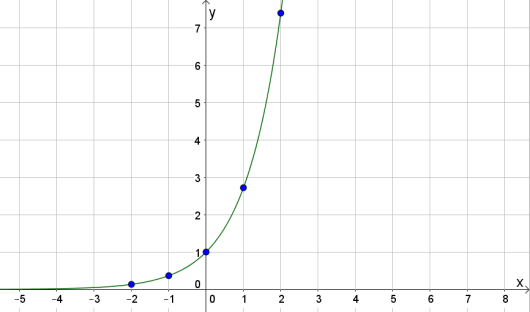
2. Finn funksjonsverdiene for når , og lag en skisse av grafen til .
FASIT
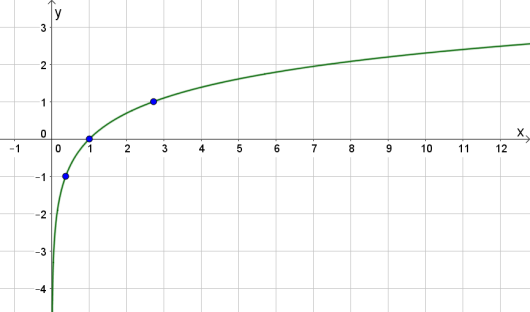
3. Finn funksjonsverdiene for når , og lag en skisse av grafen til .
FASIT
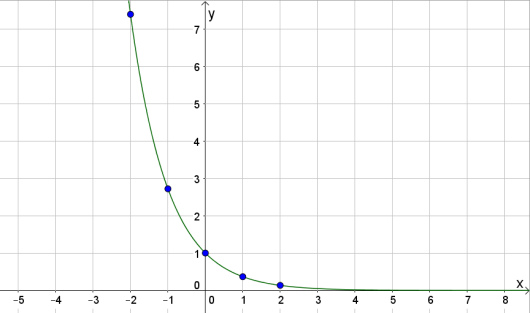
4. Finn funksjonsverdiene for når , og lag en skisse av grafen til .
FASIT
5. La og . Finn .
FASIT
6. La og . Finn .
FASIT
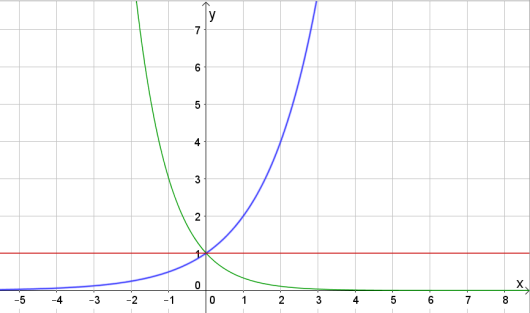
7. La for og . Skisser grafen til funksjonen i hvert tilfelle.
FASIT
FASIT
9. Skriv som en eksponentialfunksjon med som grunntall.
FASIT
Husk at og at .
10. Skriv enklere: .
FASIT
11. Skriv enklere: .
FASIT
12. La være en funksjon som representerer antall individer for en dyreart. Hvor mange individer er det ved tiden ? Hva er bæreevnen? Skisser grafen til .
FASIT
Del på Facebook
Matematikk for studenter
Funksjoner
Består av:
- Funksjonsalgebra og omvendte funksjoner
- Funksjoner og polynomer
- Eksponential- og logaritmefunksjoner