Trigonometriske formler
Ut fra symmetrien til enhetssirkelen kan vi enkelt bevise en rekke nyttige trigonometriske formler.
MatRIC: Trigonometriske identiteter
Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC
Teorem 1. Trigonometriske formler
For alle vinkler har vi:
| 1a. | 1b. | |||||
| 2a. | 2b. | |||||
| 3a. | 3b. | |||||
| 4a. | 4b. | |||||
| 5a. | 5b. | |||||
| 6a. | 6b. |
Bevis
Det er på ingen måte nødvendig å gå rundt å huske alle disse formlene. Med litt trening går det svært raskt å utlede dem, kanskje til og med i hodet, når du trenger dem. Som illustrasjon beviser vi et par av punktene her.
Teorem 1-1a og 1b:
Å addere til en vinkel, er det samme som å gå en ekstra runde rundt enhetssirkelen. (Husk at tilsvarer .) Derfor vil både og forbli uendret når man legger til .
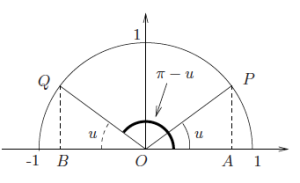
Teorem 1-4a:
På figuren under har vi tegnet inn vinklene og i en enhetssirkel. På grunn av symmetri, er trekantene △ og △ likeformede. Spesielt er |OA| = |OB|. Punktene og har altså lik absoluttverdi, men forskjellig fortegn, og vi får at
En av de viktigste trigonometriske formlene er enhetsformelen. Den er en reddende engel i mange oppgaver, så sørg for å bli god venn med denne:
Teorem 2. Enhetsformelen
For alle gjelder relasjonen .
Bevis
.
Formlene i Teorem 3 får man også bruk for rett som det er. Det kan være lurt å kunne dem utenat, i særdeleshet formlene for og .
Teorem 3.
Formlene for og .
Spesielt får vi for :
MatRIC: Utledning av summeformler
Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC
Del på Facebook
Lynkurs 11.-13.trinn
Trigonometri
Består av:
- Trekanter
- Sinus, cosinus og tangens
- Eksakte verdier
- Klara finner eksakte verdier
- Trigonometriske formler
- Grafene til sin x, cos x og tan x
- Arealsetningen
- Sinussetningen
- Cosinussetningen
- Trigonometriske likninger
- Mer kompliserte likninger
- Periodiske funksjoner
- Derivasjon av trigonometriske funksjoner
- Omskriving til standardform