Grader vs. radianer
Som oftest i vanlige geometrioppgaver måler vi som kjent vinkler i grader. Til de fleste andre matematiske formål er det derimot et annet vinkelmål som viser seg å være bedre egnet, nemlig absolutt vinkelmål.
Tenk deg en sirkel med radius . Omkretsen er da lik . Det er derfor naturlig å si at en runde i sirkelen tilsvarer radier, eller «radianer». Målt i grader, er en runde lik , slik at radianer .
Vi kan måle alle vinkler på denne måten.
Definisjon. absolutt vinkelmål radianer.
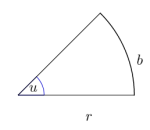
Det absolutte vinkelmålet til vinkelen er tallet , der er buelengden, og er radien. Legg merke til at siden både og er lengder, vil lengdebenevningene forkortes mot hverandre i brøken , slik at det absolutte vinkelmålet blir et ubenevnt tall. Likevel sier vi ofte at er målt i radianer.
Du lurer kanskje på hva i all verden vi skal med en ny måte å måle vinkler på, når vi allerede har grader. En av hovedgrunnene er at mange formler (f.eks. derivasjonsformler) blir mye enklere og penere med absolutt vinkelmål. En annen grunn er at vi slipper å tenke på benevninger, siden absolutt vinkelmål er ubenevnt.
Det finnes en grei formel for å gå fra grader til radianer, og omvendt:
Omregningsformel
Anta at er en vinkel målt i radianer, og at er den samme vinkelen målt i grader. Da har vi
Bevis
Siden må forholdstallene og være like, det vil si at . Multipliserer vi med på begge sider av denne likheten, får vi formelen i teoremet.
For de vanligste vinklene bør du kunne veksle mellom grader og radianer uten noe særlig nøling. I hvert fall når det gjelder disse vinklene:
Noen vanlige vinkler uttrykt i grader og radianer
| , | , | , | , | , | . |
Del på Facebook