Å bruke konjugatsetningen
Vi har allerede sett noen eksempler på bruk av første og andre kvadratsetning. På denne siden skal vi også bruke den tredje, nemlig konjugatsetningen.
Når man er godt kjent med konjugatsetningen ser man med en gang at man kan forenkle et uttrykk som :
Å bli flink til å kjenne igjen slike ting som dette krever trening, så vi går rett på og ser på et par eksempler der konjugatsetningen hjelper oss.
Eksempel 1
Skriv uttrykket enklere:
Løsning. Begynner man å gange ut her, er det lett å gå seg vill og ende opp med feil. I stedet ser vi at vi kan sette parenteser litt lurt, slik at konjugatsetningen kan brukes:
I nest siste overgang brukte vi også 2. kvadratsetning for å regne ut .
Vi tar med et eksempel til, litt mer omfattende enn det forrige. Her bruker vi alle tre kvadratsetningene «motsatt vei»:
Eksempel 2
Faktorisér uttrykket
Løsning. Ideen her er å skrive uttrykket som en differanse mellom to kvadrater, for så å bruke konjugatsetningen til å faktorisere.
La oss begynne med de tre første leddene. Ser du nøye på dem, kjenner du igjen formen til høyresiden i andre kvadratsetning, med og . Det betyr altså at
Vi kan også lage et kvadrat av de tre siste leddene, etter først å ha trukket ut en minus:
Her brukte vi første kvadratsetning med og . Dette betyr at vi kan skrive det opprinnelige uttrykket som . Fordi dette er en differanse av to kvadrater, kan vi faktorisere ved å bruke konjugatsetningen.
Vi får at
Del på Facebook
Lynkurs 11.-13.trinn
Andregradslikninger
Består av:
- Kvadratsetningene
- Å bruke konjugatsetningen
- Å fullføre kvadratet
- Faktorisering av andregradsuttrykk
- abc-formelen
- Uoppstilte andregradslikninger
Begrep
-
Første kvadratsetning
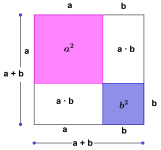
Første kvadratsetning sier at
.
-
Andre kvadratsetning
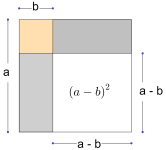
Andre kvadratsetning sier at
.
-
Konjugatsetningen
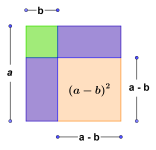
Konjugatsetningen kalles også tredje kvadratsetning:
.




