Regneregler
La oss se på hvordan vi regner med prosenter. Husk at prosent er «hundredeler», men det er ikke alltid som ugjør helheten.
Eksempel 1.
I 2013 søkte omtrent undommer seg til videregående opplæring i Oslo. av den fikk første ønsket sitt oppfylt. Hvor mange ungdommer fikk første ønsket sitt oppfylt?
Nå er «helheten» , og av disse blir da en hundredel av , som er . Siden vi skal finne må vi ta og vi får .
I Oslo fikk ungdommer første ønsket sitt oppfylt.
Dette regnestykket kan gjøres enklere. av er lik
.
ungdommer fikk første ønsket sitt oppfylt.
regel
I eksempelet over er prosenten lik og «helheten» er . Regelen brukes når vi skal finne hvor mye/mange en gitt prosent utgjør av en helhet. Denne utregningsregelen bruker vi også når vi skal finne ut ny verdi for noe som har endret seg med en gitt prosent.
Endring av opprinnelig verdi - ved økning
endring av opprinnelig verdi - ved nedgang
En endring som gjør at opprinnelig verdi øker, kaller vi ofte en økning. Andre ord som brukes om dette er for eksempel være vekst, tilskudd, prisøkning og verdiøkning.
En endring som gjør at opprinnelig verdi synker, kaller vi ofte en nedgang. Andre ord som brukes om dette er for eksempel være reduksjon, rabatt og avslag.
Eksempel 2.
Prisen på en kjole var opprinnelig kr. Den ble satt ned med . Hvor mye kostet kjolen på salg?
Her har vi en endring eller et avslag på av kr
.
Da kan vi bruke at
| opprinnelig verdi | - | endring | = | ny verdi |
| opprinnelig pris | - | avslag | = | salgspris |
| - | = |
Kjolen koster 630 kr på salg.
For å finne kjolens salgspris direkte kan vi snu litt på måten vi tenker på. Med et avslag i pris på vil vi måtte betale av den opprinnelige prisen, og av kr er
.
Endring i prosent
Noen ganger får vi oppgitt opprinnelig verdi og ny verdi, og blir spurt om hvor stor endring det har vært i prosent i forhold til den opprinnelige prisen.
Eksempel 3.
Prisen på en togbillett steg fra kr til kr. Hvor mange prosent har prisen på togbilletten endret seg med?
La oss systematisere de opplysningene vi har fått:
Ny verdi = kr
Opprinnelig verdi = kr
Endring i pris = Ny verdi - Opprinnelig verdi
Endring i pris er lik
Nå må vi finne ut hvor stor andel endringen ( kr) utgjør av den opprinnelige prisen ( kr).
Andelen omregnet til prosent er
.
Billettprisen har steget med .
endring i prosent
Endring i prosent omtales også som prosentvis endring.
Eksempel 4.
I 2010 var det som søkte videregående opplæring Medier Og Kommunikasjon. I 2013 var det søkere til Medier og Kommunikasjon. Hvor stor prosentvis endring er det i antall søkere på Medier og Kommunikasjon fra 2010 til 2013?
Opprinnelig verdi: kr
Ny verdi: kr
Den prosentvise endringen er
.
Her ser vi at vi får et negativt svar. Grunnen til dette er at søkertallet har blitt mindre. Det er jo færre søkere i 2013 enn det var i 2010. Antallet søkere har sunket med eller endringen i søkertallet er .
Det viktigste når vi skal finne prosentvis endring, er å være sikker på at vi finner hva som skal settes inn for opprinnelig og ny verdi.
Del på Facebook
Begrep
-
Brøk
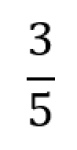
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.Eksempel : . Tallet 7 er nevneren.
-
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
-
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.




