Øvingsoppgaver med fasit

Fortegnet på vekstfaktoren i en eksponentialfunksjon bestemmer om funksjonen stiger eller synker. Er påstanden riktig? Begrunn svaret.

Du setter 25000 kr på konto med 2% rente.

a) Hvor mye har du i banken etter 10 år hvis renta er stabil, og du ikke rører pengene?

b) Finn ved regning når du har 28000 kr på konto.

Hovedindeksen på Oslo Børs var på 505,9 poeng den 18. juni 2007. Veksten siste 12 måneder hadde da vært på 42,1%.

a) Forklar hvorfor man kan finne veksten $p$ i prosent per måned dette året ved å løse likningen ${(1+\frac{p}{100})}^{12}=1,421$. Finn $p$.

b) Anta at denne veksten holder seg stabil det neste året. Hva kan man forvente at hovedindeksen vil være om 4 måneder?

c) Hva omtrent var hovedindeksen for 3 måneder siden?

d) Når passerer indeksen 600 poeng?

Siri setter 100 000 kr på langsiktig sparing. Den årlige rentefoten er på 9 %.

1. Sett opp funksjonsuttrykket f(x) som angir saldoen på sparekontoen og x er antall år.
2. Hvor lang tid tar det før beløpet er på 200 000 kr?
3. Hvor lang tid ville det ha tatt henne å spare opp il 200 000 hvis hun hadde satt inn 50 000? istedet for 100 000 kr?

Hva er forskjellen mellom en potensfunksjon og en eksponentialfunksjon?

Et laboratorium i Japan har 1000 bakterier. Denne spesifike bakteriekulturen vokser eksponentielt og dobles hver time.

1. Sett opp funksjonsuttrykket for B(t) der t står for timer.
2. Hvor mange bakterier inneholder kulturen etter 48 timer.

La f være gitt ved $f\left(x\right)=2^x$.

1. Regn ut $f(-2),f\left(0\right),f\left(2\right)$.
2. Finnes det x slik at f(x) blir negativ?

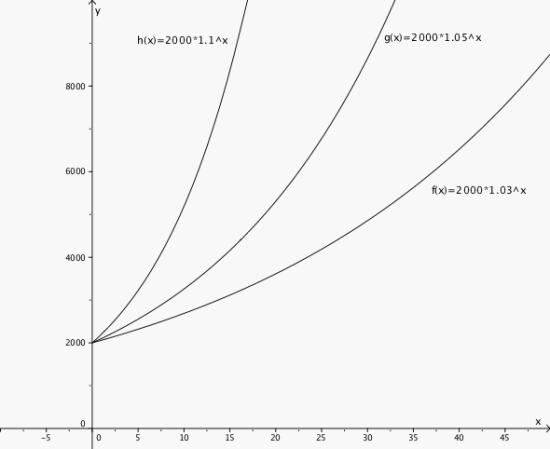
Eksponentialfunksjonene f, g og h er gitt ved

$\begin{array}{ccc}f\left(x\right)& =& 2000\cdot {1.03}^x\\ g\left(x\right)& =& 2000\cdot {1.5}^x\\ h\left(x\right)& =& 2000\cdot {1.1}^x\end{array}$

der $x\ge 0$

a) Tegn grafene til f, g og h i samme koordinatsystem.

b) Beskriv utseendet til disse grafene og forklar fellestrekk og forskjeller.

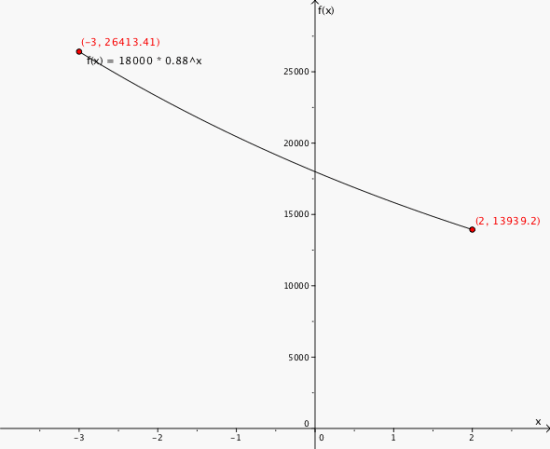
Det årlige verditapet for en moped er 12%. En tre år gammel moped er i år verdt 18 000 kroner.
a) Forklar hvorfor funksjonen f gitt ved $f\left(x\right)=18000\cdot {0.88}^x$ er en matematisk modell for verdien av mopeden om x år.

b) Hva kostet mopeden da den var ny?

c) Tegn en graf som viser verdien til mopeden fra den var ny og til den blir fem år. Hvilke forutsetninger har du lagt til grunn for å kunne tegne grafen?

Funksjonene f og g er gitt ved

$\begin{array}{c}f\left(x\right)=15\cdot {0.91}^x\\ g\left(x\right)=15\cdot {0.98}^x\end{array}$

Finn den momentane veksthastigheten for grafen til begge funksjonene for x = 3