Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
I en beholder er det 6 hvite og 4 røde baller. Vi trekker en ball tilfeldig.
a) Hva er sannsynligheten for at ballen er rød?
b) Hva er sannsynligheten for at ballen er hvit?
c) Hva er sannsynligheten for at ballen ikke er hvit?
2
|
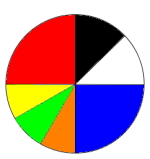
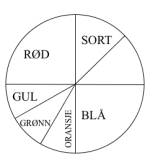
Dette er samme lykkehjulet, men de uten fargeskriver kan bruke tegningen til høyre der fargene er erstattet med fargens navn. |
|
Figuren viser et lykkehjul. Du snurrer lykkehjulet rundet én gang og ser hvilken farge det stopper på. Skriv opp en sannsynlighetsmodell for for forsøket. Hva er sannsynligheten for at lykkehjulet stopper på gul, rød eller oransje?
3
I en konkurranse blir premien gjemt i et av tre skap, A, B eller C. Gunnar vinner, men må åpne det riktige skapet for å få premien. Gunnar velger et skap, men åpner det ikke. Programlederen åpner et annet og tomt skap. Programlederen tilbyr Gunnar å bytte skap. Lønner det seg for Gunnar å bytte?
4
I en skuff ligger det 6 blå, 2 grå og 8 svarte sokker. Du tar to sokker i mørket, først en og så en til. Hva er sannsynligheten for at du får
a) to blå sokker
b) to grå sokker
c) to svarte sokker
d) to sokker med samme farge
5
Hva er sannsynligheten for at en tilfeldig valgt bokstav fra alfabetet er
a) en konsonant?
b) en vokal?
6
Du kaster én terning. Hva er sannsynligheten for at du får
a minst 4 øyne (altså 4 øyne eller mer)
b minst 2 øyne
c høyst 2 øyne (altså 2 øyne eller færre)
d høyst 4 øyne
7
27 elever fra en skole skal på tur til Nederland. Av dem har 12 elever tysk og 15 elever har fransk. Fem av elevene har både tysk og fransk. En elev trekkes ut tilfeldig for å være reiseleder. Hva er sannsynligheten for at reiselederen
a) har tysk
b) har tysk eller fransk eller begge deler
c) verken har tysk eller fransk
8
Du kaster én terning og ser hvor mange øyne du får.
a. Skriv opp utfallsrommet for forsøket.
b. Gi en sannsynlighetsmodell for forsøket.
9
Vi stokker en kortstokk. Se på kortet som ligger øverst.
a) Hva er sannsynligheten for at kortet er et hjerterkort?
b) Hva er sannsynlighetene for at kortet er en konge?
c) Et kort kalles et honnørkort hvis det er knekt, dame, konge eller ess. Hva er sannsynligheten for at kortet er et honnørkort?
10
I en bøtte ligger det 8 baller. En ball trekkes tilfeldig ut av bøtta. Utfallsrommet er U = {rød ball, blå ball, grønn ball, svart ball} og
P(rød ball) = , P(blå ball) = , P(svart ball) =
a) Bestem P(grønn ball)
b) Hvor mange røde baller, grønne baller, blå baller og svarte baller må legges hvis vi ønsker en uniform sannsynlighetsmodell?
Fasit
1
a)
b)
c)
2
P(svart)= 1/8, P(hvit)=1/8, P(blå)=1/4, P(oransje)=1/12, P(grønn)=1/12, P(gul)1/12, P(rød) = 1/4. Sannsynligheten for at lykkehjulet stopper på gul, rød eller oransje er 3/12 + 1/12 + 1/12 = 5/12.
3
Ja, i to av tre tilfeller.
4
a)
b)
c)
d) (a + b + c) =
5
a)
b)
6
a 1/2
b 5/6
c 1/3
d 2/3
7
a) 4/9 eller 44,4%
b) 22/27 eller 81,5%
c) 5/27 eller 18,5%
8
a. U = {1, 2, 3, 4, 5, 6}
b. P(1) = 1/6, P(2) = 1/6, P(3) = 1/6, P(4)= 1/6, P(5) = 1/6, P(6) = 1/6
9
a) 1/4
b) 1/13
c) 4/13
10
a)
b) For eksempel 1 grønn, 2 svarte og 1 rød. Et annet eksempel er 2 grønne, 3 svarte, 1 blå og 2 røde.