Geometri - areal og volum
I lynkurset vil vi se på hvordan vi finner areal og volum til geometriske figurer som et kvadrat, en terning og mange andre. Vi vil også se på hvordan vi i spillet Angry Birds kan vite om fuglen treffer en gris eller ikke.
Her vil du se formler og derfor regning med bokstaver. Husk at bokstavregning er en generalisering av utregninger med tall. Vi løser problemer for flere tilfeller og vi slipper å løse et problem fra bunnen hver gang det dukker opp. Det er derfor vi har formler uttrykt med bokstaver. Ofte er algebraiske formler inspirert av eller utledet av geometrien.
Hvor mye kan du om areal og volum? Ta en kort test!
Lynkurs, 8.-10.trinn
Består av:
- Tom forteller om areal
- Et kvadrat
- Et rektangel
- En trekant
- Et parallellogram
- Et trapes
- Tom forteller om overflatearealer
- Overflatearealet til en terning
- Tom forteller om volum
- Et rett prisme
- En sylinder
- Pyramider og kjegler
- En kule
- Pytagoras læresetning
- Tom forteller om formlikhet og Pytagoras læresetning
- Test deg selv i geometri (areal og volum)!
- Test deg selv i tallet π (PI)
Begrep
-
Algebra
Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.
Et algebrauttrykk kan være:
n + n + n + n + n = 5n
Her har vi lagt sammen n til sammen 5 ganger.
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Fart
Fart er tilbakelagt distanse per tidsenhet.
Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.
Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.
-
Prisme
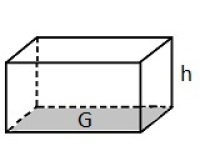
Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.
Har et prisme grunnflate G og høyde h, er volumet lik G · h. -
Radius
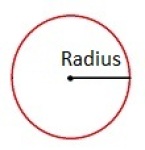
Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.
-
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.Areal:
Omkrets:




