Mia og Marius på fotballkamp
Mia og Marius er på landskamp på Ullevål stadion sammen med Nils og Arne. Det store spørsmålet denne gangen er om det er mulig å finne kampresultatene ut fra en tabell satt opp under en fotballturnering.
Historien
I løpet av et kort sekund er den pølsespisende, halvsløve folkemassen forvandlet til et brølende uhyre hvor armer og skjerf fyker i været, ketchupen spruter og popcornet triller stille og ubemerket i skjul under seteradene. Norge har skåret mål og leder 1-0 i landskampen på Ullevål stadion.
Mia og Marius står på hovedtribunen og heier på Norge av full hals. De har fått være med Nils og Arne for å se Norge rette opp den litt dårlige statistikken herrelandslaget i fotball har hatt de siste årene. Mia og Marius kjenner godt Nils og Arne, det er de som pleier å lage matematikkoppgaver til dem.
Vi har en oppgave til dere nå også, sier Nils når den verste støyen etter skåringen har gitt seg, her kommer den:
Oppgave 1
I løpet av en sesong skårer alle angrepsspillerne på et fotballag nøyaktig like mange mål. Til sammen skårer laget 49 mål. Hvor mange angrepsspillere er det på laget?
Et lite øyeblikk blir Mia og Marius mer opptatt av å løse oppgaven enn å se på kampen, men snart er de tilbake og er med på heiing, roping og synging sammen med de 25000 andre tilskuerne.
- Jeg har også en fotballoppgave til dere, skyter Arne inn. Det er ikke så vanskelig å sette opp en tabell for en fotballturnering når man kjenner alle resultatene, men tror dere det motsatte er mulig, at man kan finne resultatene når man kjenner tabellen?
Oppgave 2
I en pulje i en fotballturnering deltar tre lag. Når alle har møtt hverandre én gang så tabellen slik ut:
| Lag | Kamper | Seire | Uavgjort | Tap | Mål | Poeng |
| Driblekameratene | 2 | 1 | 1 | 0 | 3-2 | 4 |
| Fryktløse | 2 | 0 | 2 | 0 | 4-4 | 2 |
| Hodegode | 2 | 0 | 1 | 1 | 4-5 | 1 |
Hva ble resultatet av de tre kampene i pulja når du vet at seier gir 3 poeng, uavgjort gir 1 poeng og tap gir 0 poeng?
Etter pausen får Nils øye på en kollega. Hun heter Hege og kommer bort til dem.
Jaså, så det er dere som er Mia og Marius, sier hun, jeg har hørt at dere er så glad i løse oppgaver.
Det stemmer, svarer Marius, jobber du også med å lage matematikkoppgaver?
Det også, svarer Hege, i tillegg til å lage julekalendere! Dere skal få en oppgave av meg også, men den har ikke så mye med fotball å gjøre.
Oppgave 3
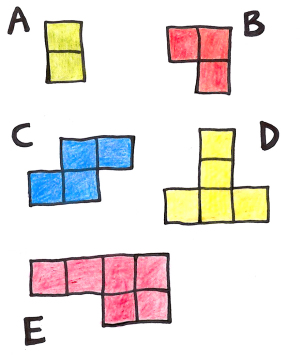
Hvis man samler sammen 4 av de 5 figurene på tegningen kan man få et kvadrat.
Hvilken figur må da utelates?
Det ble med det ene målet i kampen, Norge vant 1-0. Heia Norge!!!
Fasit
Oppgave 1
Antall angrepspillere må gå opp i 49. De eneste tallene som går opp i 49 er 1, 7 og 49. Det er opplagt ikke 1 eller 49 angrepsspillere på laget, altså er det 7 angrepsspillere som skårer 7 mål hver.
Oppgave 2
Siden Fryktløse har to uavgjorte kamper må de ha spilt uavgjort mot begge de to andre lagene, og siden Driblekameratene har én seier må de ha vunnet over Hodegode. Siden Driblekameratene har skåret ett flere mål enn de har sluppet inn må de ha vunnet kampen mot Hodegode med ett mål. Til sammen har Driblekamperatene og Hodegode skåret 7 mål, 4 av disse til sammen mot Fryktløse. Så i kampen dem imellom ble det skåret 3 mål, dvs. stillingen må ha blitt 2-1. Det gir
Driblekameratene-Fryktløse 1-1
Fryktløse-Hodegode 3-3
Hodegode-Driblekameratene 1-2
Oppgave 3
Figurene har til sammen 20 småruter. Hvis vi dropper én av dem har vi 14, 15, 16, 17 eller 18 ruter igjen, avhengig av hvilken figur vi dropper. Av disse er kun 16 et kvadrattall. Altså må vi ta bort figuren som består av 4 småruter, dvs. figur c. Resten kan vi sette sammen slik og lage et kvadrat: