Mia og Marius i Mali
Søskenparet skal besøke tante Kaja som jobber i hovedstaden Bamako i Mali. De reiser sammen med et vennepar av foreldrene, Solveig og Hugo, som har studert sammen med tante Kaja.
Historien
- Sahara er jammen stor, utbryter Mia. Det er godt vi krysser den med fly og ikke med dromedar.
- Enig, sier Marius. Men nå er vi snart fremme selv om det bare er noen timer siden flyet lettet fra Paris. Det blir spennende å være på ferie i Afrika - og i et land som delvis ligger i Sahara.
Reisefølget reiser ikke rett til Bamako. Flyet lander i den lille byen Gao øst i Mali hvor de blir møtt av Kajas kollega, doktor Maiga.
- Velkommen til Mali, hilser doktor Maiga. Håper 40 varmegrader ikke blir for varmt for dere. Dere er sikkert sultne etter turen, så kanskje vi skal starte med å spise lunsj? Har dere lyst til å spise hjemme hos meg?
- Ja, gjerne, svarer Mia og Marius i munnen på hverandre. De er spent på å se hvordan husene i Mali ser ut.
Snart sitter de på gulvet i huset til doktor Maiga. De bruker ikke stoler og bord, men sitter i en ring på gulvet og dekker med en duk i midten. De får stekt fisk som kommer fra elven Niger og masse kokt ris med grønnsaker. Hele gulvet og alle veggene er dekket av flotte tepper.
- Hvor mange tepper har du egentlig? spør Marius.
- Ja, si det, smiler doktor Maiga lurt. Dere vet sikkert at de fleste i Mali er muslimer, og at år 0 i islamsk tidsregning tilsvarer år 622 i vestlig tidsreging?
- Ja, sier Mia. Og så regner dere med måneår på 354 dager i stedet for solår på 365 dager. Et muslimsk år er altså 11 dager kortere enn det gregorianske solåret vi bruker.
-Helt riktig. Det islamske året 1436 startet 25. oktober 2014. Så da kan du sikker finne antall tepper jeg har ved hjelp av denne oppgaven, sier Maiga.
Oppgave 1
Finn det islamske året du er i 1. november 2015. Hvis du multipliserer sammen sifrene i dette året finner du hvor mange tepper doktor Maiga har i huset sitt.
Etter at de har spist hjelper doktor Maiga dem med å leie en firehjulstrekker med sjåfør som skal kjøre dem til Timbuktu. Dagen etter kjører de på en humpete sandvei inn til det mystiske Timbuktu.
- Hvorfor er Timbuktu så kjent? spør Mia.
- Det er fordi det var den viktigste og rikeste byen i området her tidligere, forteller Hugo.
- Det visste jeg, sier Marius. De eksporterte gull nordover gjennom ørkenen og importerte salt som kom fra Sahara. Tidligere var salt nesten like mye verd som gull.
- Nettopp, sier Solveig. I Europa hadde mange hørt om gullbyen Timbuktu, men det var ingen europeere som kom levende tilbake derfra før i 1829. Det var kanskje den vanskeligste byen i verden å komme til.
Dagen etter treffer de Dicko. Han tilhører tuareg-folket som bor i ørkenen, og er kledd i en fin lyseblå drakt og mørkeblå turban. Dicko har nettopp kommet til Timbuktu med salt fra Sahara. Saltet er store rektangulære blokker som man kan kutte biter av.
Tenk, i gamle dager var dette nesten like mye verd som gull. Da måtte den biten være verd mange penger, sier Mia, hun greide nesten ikke å løfte på den store saltplata.
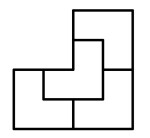
- Det var verdifulle plater i gamle dager, sier Dicko. I en gammel historie fortelles det om en far som hadde et stort stykke salt han ville at de 4 barna hans skulle dele. Men de fikk bare dele saltplata dersom de kunne dele den i fire like store biter som alle så like ut, fortsetter Dicko og tegner en figur av saltplata i sanden.
- Jeg tror jeg vet hvordan de gjorde det, sier Mia.
Oppgave 2
Figuren Dicko tegnet i sanden så slik ut:
Kan du dele figuren i fire like store deler som alle har samme form?
- Det var imponerende, sier Dicko da han hører Mias løsning. Som en premie kan dere få være med på en ridetur i ørkenen hvis dere vil. Vi kan bruke dromedarene mine.
- Åja, jubler Mia og Marius, klart vi vil.
Snart gynger det lille følget avgårde på fem dromedarer. Mia og Marius rir bakerst og storkoser seg over å reise med ørkenens skip. Etter en stund hvisker Mia til Marius:
- Ser du at Dicko, Solveig og Hugo hele tiden bytter rekkefølge på hvem som rir som nummer 1, 2 og 3? Hvor mange forskjellige rekkefølger kan de egentlig ri i?
- Det vet jeg, sier Marius. Men hvor mange mulige rekkefølger blir det dersom jeg også rir sammen med dem, slik at det er fire stykker som kan bytte plass?
Oppgave 3
Hvor mange forskjellige rekkefølger kan det være på tre dromedarer? Og hvor mange forskjellige rekkefølger kan det være på fire dromedarer?
Dagen etter drar Mia, Marius, Solveig og Hugo videre til en by som heter Bandiagara. Her møter de tante Kaja og drar sammen på fottur i Dogon-land.
- Dette er et spennende område! sier tante Kaja. Menneskene som bor her, har både sin helt spesielle måte å telle på og sin egen kalender. I Dogon-land har de en uke på 5 dager i stedet for 7 dager som vi er vant til.
- Oj! sier Mia. Da blir det jo hele 73 uker i ett år. Men det må jo være vanskelig å bruke begge kalendrene samtidig.
- Ja, det er det, svarer tante Kaja. Den landsbyen vi skal besøke har for eksempel marked den første dagen i hver 5-dagersuke. Det er veldig forvirrende for folk utenfra og ikke alltid lett å vite når det er marked. Jeg var i landsbyen 1. januar 2004 på vår kalender, og da var det marked der.
- Hm, sier Marius. Er det noen av dere som kan finne ut neste gang det vil være marked i landsbyen den 1. januar?
Oppgave 4
Hvis 1. januar 2004 falt på den første dagen i 5-dagersuken, hvilken dag i 5-dagersuken faller da 1. januar 2005 på? (Husk på at i et skuddår er det 366 dager)
Fasit
Oppgave 1
25. oktober 2014 startet år 1436. Et muslimsk år er på 354 dager, 11 dager kortere enn det gregorianske året vi bruker. 1. november 2015 er 372 dager etter 25. oktober 2014. Dette betyr at 1. november 2015 er vi i året 1437.
For å finne antallet tepper doktor Maiga har, multipliserer vi sifrene i årstallet: .
Doktor Maiga hadde 84 tepper.
Oppgave 2
Oppgave 3
Tre dromedarer A, B og C kan gå i 6 forskjellige rekkefølger.
ABC, ACB, BAC, BCA, CAB, CBA. (Kan regnes ut som 3·2·1 = 6)
Hvis en fjerde dromedar D skal plasseres, kan den gå som nr. 1, 2, 3 eller 4 i hver av rekkefølgene ovenfor. Det blir tilsammen 24 muligheter)
DABC DACB DBAC DBCA DCAB DCBA
ADBC ADCB BDAC BDCA CDAB CDBA
ABDC ACDB BADC BCDA CADB CBDA
ABCD ACBD BACD BCAD CABD CBAD
(Kan regnes ut som 4·3·2·1 = 24)
Oppgave 4
I et år som ikke er skuddår er det 365 dager. Regner vi i 5-dagersuker blir det nøyaktig 73 uker. Siden 2004 er et skuddår inneholder det 366 dager. Det vil si at i 2004 blir det plass til den første dagen av uke nummer 74. Derfor må 1. januar 2005 bli dag nummer 2 i 5-dagersuka.