Mia og Marius i Kina
Mia og Marius har nettopp kommet hjem etter å ha vært på ferie i Kina og Japan. Det var en spennende tur. Blant annet var de på besøk i byene Shanghai og Sapporo.
Historien
- Jammen var det vanskelig å lære seg de kinesiske skrifttegnene, sier Marius.
Nå sitter de og ser på bilder fra turen og snakker om hva de opplevde.
- Jeg synes vårt alfabet er mye enklere enn å skulle lære mange tusen skrifttegn, sier Mia. Men det var bra for oss at de brukte de tallene vi bruker, det gjorde de jo ikke tidligere.
- Nei. Se her, sier Marius og peker på noe på et bilde. I det 700 år gamle manuskriptet vi var og så på, har de brukt andre talltegn. Den figuren må være Pascals trekant.
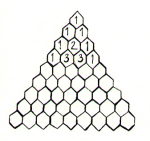
- Her står det hvordan man lager den, sier Mia og peker på dataskjermen. Du starter med et 1-tall i toppen, og så lager du tall under i et trekantmønster slik at et nytt tall er summen av de som står rett over. Se her. Mia tar fram et annet bilde av det kinesiske manuskriptet og viser Marius hvordan skjemaet skal fylles ut.
Oppgave 1
Fyll ut Pascals trekant etter reglene som Mia forklarte.
- Ja, dette var jo ganske enkelt, sier Marius. Ser du forresten at på skrå nedover i en av radene står tallrekka? 1,2,3,4,5,6,... Og ser du hvordan du kan bruke trekanten til å finne svar på regnestykkene
1+2=
1+2+3=
1+2+3+4=
1+2+3+4+5=
osv.?
Oppgave 2
Prøv å finne et mønster i Pascals trekant som gjør at du enkelt kan finne svarene på regnestykkene til Marius. (Hint: Regn ut svarene og se om du kan finne de samme tallene i trekanten.)
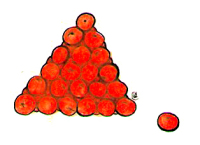
- Å, se på dette bildet som vi tok i Shanghai. Det er av han kjøpmannen som hadde lagt opp appelsinene sine i pyramideform med en trekant som grunnflate. Tror du han visste på forhånd hvor mange appelsiner han trengte for å lage en pyramide?
- Tja, kanskje? Men hvordan kunne han vite det? tror du det er en måte å regne ut det på?
- Det er det sikkert! Vi kan prøve oss fram. Vi begynner med å lage de minste pyramidene. Den aller minste pyramiden består bare av 1 appelsin. Den nest minste har 3 appelsiner i bunnen og 1 på toppen. Den neste pyramiden har 6 appelsiner i bunnen, 3 i neste lag og 1 på toppen. Og så fortsetter vi.
- Visste du forresten at appelsin egentlig betyr "eple fra Kina"? spør Mia.
Portugiserne tok appelsiner med seg hjem til Europa fra Kina etter at de hadde oppdaget sjøveien hit. I Europa hadde ingen sett en lignende frukt, så i Tyskland og Nederland kalte man dem for "Apfel aus China" - for epler visste alle hva var. Senere ble ordene trukket sammen til å bli ordet appelsin.
Oppgave 3
Kan du finne ut hvor mange appelsiner som trengs for å lage en pyramide med 4 lag? Og hvor mange som trengs for å lage en med 7 lag? (Hint: det går an å bruke Pascals trekant her også.)
- Her er et bilde fra Sapporo, sier Marius. Det var der det var Olympiske leker i 1972. Husker du forresten at gatene der krysset hverandre slik at mønsteret nesten ble som et sjakkbrettmønster?
- Ja, vi bodde i det hotellet på gatehjørnet, sier Mia mens hun peker på bildet. Husker du hvor mange ganger vi gikk ned til iskrembaren som lå noen gater lenger nede?
- Klart jeg gjør det, og jeg husker også at vi hadde en konkurranse om at hver gang vi skulle ned måtte vi gå en vei som ikke var helt lik en vi hadde gått tidligere, sier Marius.
- Ja, også var det bare lov å gå rett østover eller rett sørover, aldri i motsatt retning.
- Og vi fikk det til hver gang, sier Marius. Men hvor mange forskjellige veier var det egentlig mulig å gå, tror du?
Oppgave 4
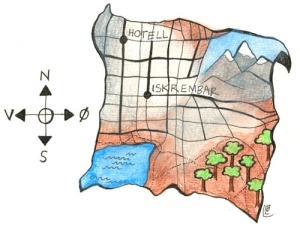
Her ser du et kart over området der Mia og Marius bodde. Hotellet og iskrembaren er tegnet inn. Hvis du bare har lov å gå i retningene som pilene viser hvor mange forskjellige ruter er det da mulig å velge fra hotellet til iskrembaren?
Fasit
Oppgave 1
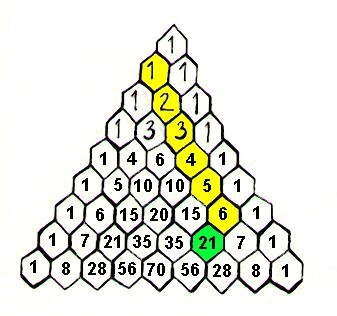
Fargene som er markert i figuren tilhører forklaringen til oppgave 2.
Oppgave 2
For å finne f. eks. svaret på 1+2+3+4+5+6 følger vi den gule "stien" i trekanten fra oppgave 1 og kan lese svaret rett ned til venstre i ruta markert med grønn farge. Slik kan vi fortsette nedover i trekanten for å finne svaret på summen av de 11 første tallene også.
Ved å skrive opp de 4 neste radene vil vi finne svaret 1+2+...+10+11 = 66.
Oppgave 3
Til 4 lag trengs 20, til 7 lag trengs 84.
Vi kan bruke Pascals trekant igjen. Ved å følge stien rett under den gule i oppgave 1 (med tallene 1, 3, 6, 10 osv.) kan vi telle oss nedover det antall lag vi ønsker å finne summen til. Det fjerde tallet nedover er 10 og skrått ned til venstre står 20, som er summen av de 4 lagene. Det sjuende tallet er 28, så da blir summen 84 (som er 56+28).
Oppgave 4
Her kan vi bare telle oss frem, det er 10 veier som er mulig å velge.