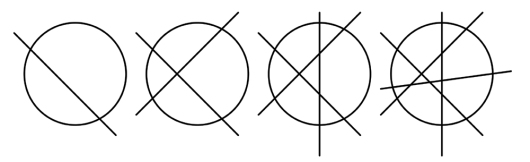Mia og Marius på hyttetur i Sakkesdalen
Mia og Marius er på hyttetur og deltar på grandonkel Ragnars påskerenn. Inne i hytta finner de hytteboka, og der fant de et problem som Ragnar hadde skrevet sammen med Kong Olav. De må tenke logisk og kunne kjenne igjen tallmønster for å klare å knekke nøttene de får.
Historien
- Neste mann ut er Marius!
- Hvilken Marius?
- Store Marius.
Deltakerne i Påskeskirennet i Sikkilsdalen står på toppen av bakken og gjør seg klare. Mia og Marius er på hytta til Grandonkel Ragnar i Sikkilsdalen, eller Sakkesdalen som Ragnar kaller den fordi hytta for noen år siden begynte å synke litt ned i grunnen på den ene siden. De har vært her alle påskedagene, og nå er de med på det tradisjonelle påskeskirennet for alle påskegjestene. Tidligere år hadde alltid Marius vært den eneste med det navnet, men i år var det en liten tass med samme navnet som ham som var en av de litt mer spesielle gjestene. Onkel Ragnar bor rett nede i bygda og har hatt hytte i Sakkelsdalen i mange år. I tillegg har han, og faren hans før ham, drevet landhandleri, og i mange år leverte han varer når kongefamilien var på påskeferie.
Mia og Marius hadde sittet om kveldene på hytta og lest i hytteboka. Spesielt en side hadde de merket seg. Det var noen år siden nå. Onkel Ragnar hadde hatt hele kongefamilien på besøk til lunsj. Ragnar og Kong Olav hadde skrevet i hytteboka sammen, og siden onkel Ragnar i likhet med resten av familien til Mia og Marius var veldig glad i små oppgaver og problemer hadde han ikke kunnet dy seg her heller. Kong Olav knegglo godt da de skrev dette, fortalte onkel Ragnar, men resten av familien hans hadde visst ikke skjønt poenget. Her er det onkel Ragnar skrev:
"I dag har vi besøk av nabofamilien: bestefar, mor, far og to barn. De har sittet rundt bordet og spist lunsj sammen med eierne av hytta, Ragna og undertegnede. I alt sju stykker.
Eldstemann i laget hadde ikke noen av sin egen familie på noen side.
Barna var av gode grunner plassert lengst mulig fra hverandre.
Ingen av hunkjønn satt ved siden av hverandre.
Dette gir to muligheter, og kun de som var tilstede skal vite hvilken av dem det var."
Mia og Marius hadde funnet ut hvordan de hadde sittet og prøvd flere ganger på å få onkel Ragnar til å røpe hvilken av de to mulighetene som var den riktige. Det ville han ikke, det eneste han ville si var at kona hans var blitt litt flau da hun skumpet borti hånda til minstemann slik at han sølte tomatsuppe på buksa si.
Oppgave 1
Kan du ut i fra opplysningene over finne ut hvem som satt hvor under lunsjen?
- Kom og spis pizza, ropte onkel Ragnar, og det kunne jo smake godt etter all denne skigåinga. Onkel Ragnar hadde stekt en stor rund pizza og nå var han i ferd med å skjære den opp.
- Stopp litt, sa han plutselig, - vet dere hvor mange biter vi kan dele pizzaen i med ett rett kutt? Det synes Mia og Marius var et enkelt spørsmål, men de følte på seg at det snart ville bli vanskeligere.
- Og med to rette kutt, hva er det største antall biter vi kan få da? Og med tre, og fire og fem og så videre? Fram med papir og blyant, og pizzaen var nesten blitt kald før Mia og Marius hadde svaret.
Oppgave 2
Hva er det største antall biter vi kan dele en pizza i med ett rett kutt? Med to rette kutt? Og tre? Fire? Fem? Og videre?
- Nå er det leggetid, sa onkel Ragnar, - dere skal tidlig opp i morgen, vet dere, det er avmarsj herifra allerede klokka ni, men dere kan likevel ta med dere en liten oppgave i senga. Dere husker at tante Ragna var så glad i dyr. Vi har jo hatt dyr bestandig. Men da jeg traff tante Ragna hadde hun tre forskjellige typer kjæledyr: katt, hund og papegøye. Jeg kan fortelle dere at alle unntatt to var katter, alle unntatt to var hunder og alle unntatt to var papegøyer. Hvor mange kjæledyr hadde hun i alt?
- Den fikser vi raskt, sa Marius og hoppet opp i overkøya.
Oppgave 3
Tanta Ragna hadde tre forskjellige typer kjæledyr, katt, hund og papegøye. Alle unntatt to var katter, alle unntatt to var hunder og alle unntatt to var papegøyer. Hvor mange kjæledyr hadde hun i alt?
Mia og Marius sov godt den natta. Masse fjelluft og alle onkel Ragnar sine oppgaver hadde tatt på, og de hadde klart å løse alle sammen. Men ikke før hadde de våknet dagen etter før onkel Ragnar var på pletten igjen.
- Dere får ikke frokost før dere har gitt meg svaret på følgende problem. For noen år siden hadde vi flere forskjellige konkurranser på påskeaften, 15 for å være helt nøyaktig. Det var premie til vinneren i hver konkurranse. Noen vant flere konkurranser og noen vant ikke i det hele tatt. Til sammen ble det altså delt ut 15 premier. Ingen fikk like mange premier. Hva er det største antall personer som kan ha fått premie?
Den dagen satt frokosten langt inne, men til slutt greide de onkel Ragnars frokostnøtt.
Oppgave 4
Finn svaret på onkel Ragnars frokostnøtt!
Fasit
Oppgave 1
Eldstemann må ha vært bestefaren, og han satt da mellom Ragnar og Ragna. Barna må ha sittet dernest med mor og far mellom seg. Siden ingen hunkjønn satt ved siden av hverandre må rekkefølgen ha vært bestefar, Ragna, sønnen, mor, far, datteren, Ragnar og tilbake til bestefaren igjen. Det er to muligheter, mot høyre eller mot venstre. Tilleggsopplysningen tyder på at Ragna satt til høyre for sønnen siden hun sannsynligvis har skumpet til den nærmeste hånda og det har tydeligvis vært høyrehånda.
Oppgave 2
Ett kutt gir to biter, to kutt kan gi fire biter, tre kutt kan gi 7 biter mens 4 kutt kan gi 11 biter.
Det neste kuttet kan maksimalt øke antall biter med 5 og deretter med 6, så generelt har vi 1+1+2+3+4+5+6+7+ +N når vi gjør N kutt.
Oppgave 3
Det var til sammen tre dyr, én av hver. Alle unntatt to er en.
Oppgave 4
1+2+3+4+5=15, så det minste antall vinnere er 5, én får en, én får to, én får tre, én får fire og én får fem.