Mia og Marius på fisketur
Mia og Marius er på fisketur med pappa. Pappa er "storfisker" og serverer den ene fiskehistorien etter den andre. Men ved å regne litt på opplysningene de får, er de sikre på at pappa har det med å overdrive litt. Hvordan de veier fisken uten vekt får du vite i denne historien.
Historien
Når vi møter søskenparet Marius og Mia igjen er de på fisketur med far. Far er "storfisker", en sånn som alltid legger på litt ekstra når han skal fortelle hvor store fisker han har fått.
De har reist til Seljordsvannet og bruker robåt for å komme seg utpå. Mens Marius og Mia sitter ved hver sin åre og ror utover vannet sitter far og mimrer om tidligere tiders storfangst.
- Dere skulle sett den fisken jeg fikk sist gang jeg var her, den var minst 30 cm - mellom øynene altså - sier far og ser drømmende utover det stille vannet.
- Du Mia, sier Marius, er det ikke et visst forhold mellom avstanden mellom øynene og lengden av en ørret?
- Jo, sier Mia, normalt er forholdet mellom avstanden mellom øynene og lengden av fisken som 1 til 15. - Du far, sier Mia og smiler lurt, det må minst ha vært Seljordsormen du fikk sist gang hvis den var så lang som du påstår!
Oppgave 1
Hvis fars historie var sann, hvor lang var fisken han fikk?
Etter et par timer hvor Mia og Marius har halt opp den ene fisken etter den andre får også far noe på kroken. Han setter så klart i gang med å skryte om hvor stor og tung denne fisken må være - det kan jo hende at det til og med er selveste Seljordsormen han har fått på kroken!
Etter ganske mye strev får han fisken ombord i båten og stolt utbryter han at denne fisken veier i alle fall over 5 kg. Det tror ikke Marius og Mia noe på, den ser mye mindre ut enn 5 kg. De krangler en stund og finner til slutt ut at for å få en ende på diskusjonen, må de prøve å finne ut om fisken veier mer eller mindre enn 5 kg.
- Er det ikke slik at 1 liter vann veier omtrent 1 kg, sier Mia til Marius.
- Jo, svarer Marius og peker på to bøtter som står i båten, den ene tar 3 liter og den andre tar 7, men ingen av bøttene har litersmerker.
- Hvis vi hadde klart å måle opp nøyaktig 5 liter vann, så kunne vi brukt en vektstang for å finne ut om fisken som far fikk er tyngre eller lettere enn 5 kg.
Oppgave 2
Hvordan kan Mia og Marius måle opp nøyaktig 5 liter vann?
Mia og Marius holder hver sin ende av vektstanga. I den ene enden henger de bøtta med 5 liter vann, i den andre enden er fisken bundet opp. De slipper samtidig og ser bort på far. Han trekker på skuldrene, smiler litt fårete og innrømmer at Mia og Marius hadde rett hele tiden.
På veien hjem møter de tre venner. Den første de møter får halvparten av fangsten pluss en, den neste de møter gir de halvparten av det som er igjen pluss en og den tredje de møter får halvparten pluss en. Etter dette har far, Mia og Marius igjen en fisk som de har bestemt seg for at skal være middagen denne dagen.
Oppgave 3
Hvor mange fisk fikk de tilsammen?
- Neste gang, sier far, da nøyer vi oss ikke med fisk. Vi prøver å fange sjøormen i Seljordsvannet! Marius og Mia ser oppgitt på hverandre og lurer på hvordan han har tenkt seg at det skal foregå.
- Jo, nå skal dere høre sier far og veiver hektisk med armene. Han tegner opp en trekant i lufta og forklarer at det i følge et gammelt sagn skal være slik at dersom en skal fange ormen i Seljordsvannet må det skje med garn hvor maskene er trekantet. Sagnet sier dessverre ingen ting om hvor stor eller liten maskevidden skal være eller hvordan trekantene skal se ut, men de må være slik at alle trekantene i garnet har samme form. Vi må lage flere ulike garn og forsøke oss fram!
Oppgave 4
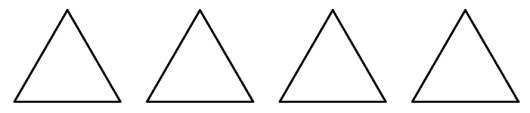
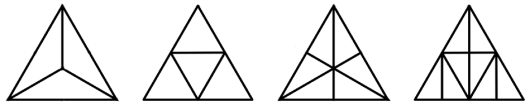
Ovenfor ser du fire likesidete trekanter. Del trekanten inn på følgende måte:
- den første skal deles slik at det blir 3 like store trekanter med samme form,
- den neste skal deles slik at det blir 4 like store trekanter med samme form,
- den deretter skal deles slik at det blir 6 like store trekanter med samme form,
- den siste skal deles slik at det blir 8 like store trekanter med samme form.
Fasit
Oppgave 1
Hvis forholdet mellom avstanden mellom øynene og lengden av fisken er som 1 til 15 betyr det at en fisk med 1 cm mellom øynene vil være 15 cm lang. En fisk med 2 cm mellom øynene vil være 15 cm + 15 cm = 215cm = 30 cm og en fisk med 30 cm mellom øynene (som far hevder) vil være 3015 cm = 450 cm = 4,5 m i lengde.
Oppgave 2
Fyll 3-literen opp tre ganger og slå dette over i 7-literen. Da sitter du igjen med 2 liter i 3-literen. Tøm 7-literen og slå de 2 literne over i 7-literen. Fyll opp med enda en 3-liter i 7-literen. Da er det 5 liter der.
Oppgave 3
Hvis vi starter "bakfra" med den fisken Mia og Marius skulle ha til middag så var denne ene + den de gav fra seg tilsammen halvparten av det de hadde igjen etter at de hadde gitt bort fisk til person nummer 3 (nemlig det dobbelte av 1+1 fisk - 4). Den andre personen de møtte fikk 5 fisk, den første de møtte fikk 12 fisk. Da hadde de først 12 + 5 + 4 + 1 = 22 fisk.