Mia og Marius på rakettbasen på Andøya
Mia og Marius er på sommerferie på Andøya og har fått lov til å besøke rakettskytefeltet. En ny forskningsrakett skytes opp fra rakettutskytningsbasen og sjefen på basen, Larsen, forteller søskenparet at raketten skal hjelpe oss til å bedre å forstå nordlyset.
Historien
5-4-3-2-1-Fyr!
Det flammer ut av rumpa på raketten, og så skyter den fart mot himmelen. En stund kan de se ildkula høyt der oppe før den forsvinner i skylaget.
- Den raketten kunne sikkert ha gått helt til månen, sier Mia. Marius er ikke enig.
- De rakettene som skal til månen er mye større og kraftigere, det er alt for langt for en sånn liten rakett.
- Det er nok riktig, det, sier Larsen, men vet dere hvor langt det er til månen?
Ingen av barna vet svaret, men de tipper likevel. Ei jente fra Stranda er nærmest, hun tipper 350 000 km.
- Det er nesten helt riktig. sier Larsen, men det varierer noe siden månen går i en ellipsebane rundt jorda. Gjennomsnittsavstanden er rundt 375 000 km. Vil dere ha et "fun fact" om avstanden til månen?
- Ja, svarer Marius.
- Hvis vi tar det papiret her, som er omtrent 0,05 mm tykt, og bretter det dobbelt mange nok ganger, så kommer vi til månen. Dette går selvfølgelig ikke an, så det vi egentlig gjør er å finne ut hvor mange lag vi får etter et visst antall brettinger og så gange med tykkelsen.
Oppgave 1
Hver gang vi bretter papiret får vi dobbelt så mange lag. Hvis vi hadde kunnet brette papiret så mange ganger vi bare ville, hvor mange ganger måtte vi ha brettet papiret for å komme til månen?
- Det er mye lenger til sola enn til månen, sier Larsen etterpå, og sola er mye, mye større enn jorda.
- Hvor mye større er den? spør Marius.
Oppgave 2
Diameteren til solkula er omtrent 109 ganger jorddiameteren. Men hvis vi sammenlikner volumene på sola og jorda er det plass til omtrent 1 300 000 jordkloder inni sola. Kan dere forklare hvorfor det tallet er så myhe større enn 109?
- Nei, nå får vi komme oss litt ned på jorda. Skal vi gå inn i hovedbygningen og spise litt formiddagsmat?
Barna er sultne etter en begivenhetsrik formiddag, så Larsen trenger ikke å be dem to ganger.
- Som dere ser holder vi på å bygge en ny messebygning, helt nede ved vannkanten. Vi har satt opp 9 stolper som bygningen skal stå på, sånn som på tegningen under. For å få det skikkelig solid skal vi bruke fire tjukke bjelker som skal ligge på kryss og tvers over de 9 stolpene, slik at den ene fortsetter der den andre slutter. Klarer dere å tegne det? De fire bjelkene er helt rette og skal gå innom alle de 9 stolpene. De kan gjerne krysse hverandre. Det får vi til med litt sveising.
Oppgave 3
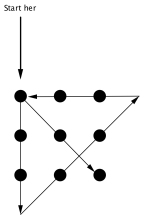
På figuren ser du 9 punkter som markerer de 9 stolpene. Kan du trekke 4 rette linjer slik at de går innom alle 9 punktene, uten å løfte blyanten fra papiret?
På vei opp til formiddagsmaten møter de en gjeng som skal ut og trene på syklene sine.
- Å, det er den dagen i dag, utbryter Larsen, alle fire er ute og sykler.
- Pleier de ikke det? spør Marius.
- Vel, svarte Larsen, dere skjønner at de er fire stykker med i sykkelgruppa på basen. Men de er ikke like ivrige. Én av dem sykler hver dag, én annenhver dag, én tredjehver dag, og fjerdemannen sykler hver fjerde dag. Med jevne mellomrom skjer det at de sykler sammen alle fire. Kan dere finne ut hvor ofte det skjer?
Oppgave 4
I sykkelgruppa er det 4 medlemmer.
- Én av dem sykler hver dag,
- én sykler annenhver dag,
- én sykler tredjehver dag,
- og én sykler fjerdehver dag.
Hvor ofte sykler alle sammen?
- Oppgaven er løst og i morgen skal vi reise hjem, sier Mia.
- Kanskje vi skulle haiket med en rakett, foreslår Marius. Men de får nok komme seg hjem på en mer vanlig måte.
Fasit
Oppgave 1
Bunken må brettes 43 ganger(!).
2 x 0,05 mm = 0,1 mm
2 x 0,1 mm = 0,2 mm
2 x 0,2 mm = 0,4 mm
2 x 0,4 mm = 0,8 mm
2 x 0,8 mm = 1,6 cm..... osv. helt til vi får 375 000 km.
Oppgave 2
Det er fordi volumet av en kule inneholder radien ganget med seg selv tre ganger.
Oppgave 3
Oppgave 4
Hver 12. dag, fordi 1223 = 12, som er minste felles multiplum av 1, 2, 3 og 4.