Mia og Marius feirer 17. mai
Det er 17. mai og Mia og Marius er tidlig oppe. De finner ut av hvor mye is og brus de får ut av 100 kr. og de deltar i matematikk-konkurransen i parken nedenfor huset sitt.
Historien
- Yess!
Marius ga fra seg et gledesrop da han trakk opp rullgardinen på rommet og konstaterte at sola skinte. Regnvær på 17. mai var det verste han visste. Mia sov fortsatt, men Mamma var allerede i gang med å stryke noe fintøy.
- Vet du når sola sto opp i dag? spurte hun. Marius ristet på hodet.
- Vel, fortsatte Mamma, nå er klokka tre minutter på sju, og tiden fra soloppgang til nå er halvparten så lang som tiden fra midnatt til soloppgang! Kan du finne svaret da?
Marius tenkte seg om og begynte å regne.
- Vet det!
Mia dukket plutselig opp i døra, tidsnok til å få med seg spørsmålet. Nå hadde hun svaret klart.
- Æsj, hun regner alltid så kjapt så tidlig om morgenen, tenkte Marius, men han sa ikke noe.
Oppgave 1
Når det var dobbelt så lang tid mellom midnatt og soloppgang som mellom soloppgang og klokka tre minutter på sju, på hvilket tidspunkt sto sola opp?
Skolen til Mia og Marius skulle være med i det store barnetoget inne i byen. Elevene ble hentet av en haug med busser og fraktet til oppmarsjstedet. Etter litt venting begynte de å gå den lange veien opp mot Slottet.
- Vet dere hvilket nummer vi har i toget i år? spurte en av lærerene, og fortsatte: - Uansett om dere deler tallet på 2, 3, 4, 5 eller 6 så får dere 1 til rest. Og tallet er mindre enn 100.
Alle barna snudde seg mot Mia og Marius. De pleide å ha svaret lenge før alle andre likevel. Og ganske riktig, tallet trillet ut før noen hadde rukket å rope hurra så veldig mange ganger.
Oppgave 2
Hvilket helt tall, mindre enn 100, gir 1 i rest uansett om vi deler med 2, 3, 4, 5 eller 6?
Omsider begynte Mia og Marius sin skole å nærme seg Slottet. Oppe på slottsbalkongen sto hele Kongefamilien og vinket, slik de hadde gjort i flere timer allerede. Mia og Marius vinket tilbake med flaggene sine.
- Tror du Mette-Marit og de andre får masse is og brus på 17. mai? Eller må de bare stå der opp hele dagen?
- De har sikkert noen tjenere som løper ut og kjøper is til dem. Jeg har i hvert fall spist nok is og drukket nok brus, jeg gleder meg til vi kommer til et sted med en do. Vet du hvor mye jeg har spist og drukket?
Det visste ikke Marius, han visste egentlig ikke hvor mye han hadde spist selv engang.
Brusen koster 15 kroner og isen 12. Jeg hadde med meg 100 kroner og nå har jeg 34 kroner igjen. Resten har jeg brukt på is og brus. Kan du finne ut hvor mange jeg har kjøpt av hver?
Nå var B-mennesket Marius mer på banen enn han hadde vært i dag morges og han brukte ikke mange sekunder på å finne svaret.
Oppgave 3
Når brusen koster 15 kroner og isen koster 12 kroner, hvor mange har Mia kjøpt av hver hvis hun hadde med seg 100 kroner og har 34 kroner igjen?
På ettermiddagen på 17. mai var det alltid leker og underholdning i parken rett nedenfor huset til Mia og Marius. I år var det tilfeldigvis en matematiker med i 17. mai-komitéen og derfor var det både matematikkleker og -konkurranser. Mange syntes det var litt rart å ha det på 17. mai, det var ikke helt etter tradisjonen, men Mia og Marius synes det var helt topp. Og så vant de jo så mange premier. En av oppgavene de fikk var:
Oppgave 4
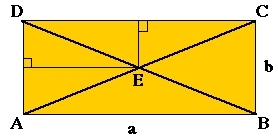
Kan du dele rektangelet med én rett strek, uten å måle opp og slik at de to delene får nøyaktig samme areal? Og kan du på tilsvarende måte ved hjelp av to rette streker dele rektangelet i fire deler, alle med like stort areal?
- Det er gøy med 17. mai, men det hender man får litt vondt i magen.
- Jeg vil jo heller si at det hender at man ikke får vondt i magen, men det er verdt det!
Fasit
Oppgave 1
Sola sto opp kl. 04:38.
Fra midnatt til kl. 06:57 er det 6 timer og 57 minutter, og denne tiden må vi dele i tre like store deler siden det skulle være dobbelt så lenge fra midnatt til soloppgang som fra soloppgang til kl. 06:57. Om vi deler 6 timer og 57 minutter på 3, får vi 2 timer og 19, minutter som blir lengden på tiden fra soloppgang til kl. 06:57. Fra midnatt til soloppgang er det 2(2 timer og 19 minutter) = 4 timer og 38 minutter.
Oppgave 2
61, se på største felles multiplum av tallene 2, 3, 4, 5 og 6, nemlig 2235 = 60, og legg til 1 slik at du får den resten du skal ha.
Oppgave 3
2 brus og 3 is her kan du bare prøve deg frem.
Oppgave 4
To like store områder med én strek trekk en av diagonalene.
Fire like store områder med to streker trekk begge diagonalene.
Ser vi på trekantene i rektangelet ser vi at AED = BEC og at CED = ABE. Vi må nå finne ut om alle arealene er like store.
Arealet av .
Arealet av .
Arealene er like store, og vi har klart å dele rektangelet i 4 like store områder.