Mia og Marius blåser såpebobler
Mia og Marius er på besøk hos onkel Einar som er fysikklærer. Han er glad i å eksperimentere og denne gangen er det såpeboblenes tur. Han utfordrer Mia og Marius til å finne ut hvor mange såpebobler de klarer å lage og til slutt får de i oppdrag å vaske bort alle såpeboblenedslagene, men det skal gjøres på en spesiell måte.
Historien
- Nå begynner blandingen å se bra ut. Mia rører i den store koppen med den tyktflytende grønne blandingen.
Mia og Marius er på besøk hos onkel Einar. Han er fysikklærer og veldig glad i å eksperimentere. Nå lager de såpebobler, Zalo, kaldt vann, noen dråper glyserol, kjøpt på apoteket og litt sukker. Så må blandingen stå og godgjøre seg før den er klar til å blåses.
- Skal vi prøve? sier Marius og dypper ståltrådringen ned i koppen. Han blåser på filmen og ut kommer en stor og fin såpeboble.
OPPGAVE 1
Mia og Marius har laget 225 g såpeboblevann. Hver såpeboble veier 1/3 gram. Hvor mange såpebobler rekker såpeboblevannet til dersom vi klarer å utnytte hver minste dråpe?
- Hvorfor blir såpeboblene trill runde, undrer Marius. Det kan onkel Einar svare på.
Han forteller at på grunn av kreftene som virker mellom molekylene i såpeboblefilmen, så vil såpeboblene prøve å få minst mulig overflate rundt den lufta som er blåst inn. Og den minste overflaten er akkurat en kuleflate.
- Men det er det ganske vanskelig å bevise, så i stedet skal dere få en annen oppgave, som ikke har så mye med såpebobler å gjøre.
Oppgave 2
Hvis vi legger sammen to tall får vi 20, og hvis vi ganger dem sammen får vi 96. Hvilke to tall tenker vi på?
Det blir mange flotte såpebobler etter hvert, kulerunde enkeltbobler og klaser hvor flere bobler hekter seg sammen. I tillegg begynner stuegulvet til onkel Einar å bli litt glatt av alle såpeboblene som har falt ned og sprukket i det de treffer bakken.
- Dere skal få en siste oppgave som dreier seg om å vaske bort alle såpeboblenedslagene. Her i stua ligger det en god del tepper. Dere skal vaske mellom alle teppene, men bare én gang hvert sted. Dere har ikke lov å løfte vaskekosten fra gulvet. Tror dere det er mulig?
Oppgave 3
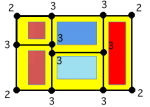
Figuren viser en skisse av stua til onkel Einar med 5 tepper. Kan du finne en vei å gå med vaskekosten som er innom alle mellomrommene mellom teppene, uten å gå noen av mellomrommene mer enn en gang? Du skal starte og slutte i øvre venstre hjørne og hele tiden holde deg på det gule og du skal ikke løfte opp kosten. Gi en forklaring.
Fasit
Oppgave 1.
225 g delt på gram er det samme som å gange 225 med 3, det vil si 675 såpebobler.
Oppgave 2.
8 og 12
Oppgave 3
Nei, det er ikke mulig.
Hvorfor ikke? La oss først tegne opp alle "veiene" vi må gå. Så ser vi på alle steder der flere veier møtes. Vi teller opp antall veier som på et sted.
Vi fører kosten fra det øverste venstre hjørnet til neste sted. Der står det 3 som betyr at tre veier møtes der. Dette er første gangen vi er på dette stedet. Nå fører vi kosten videre. Før eller senere kommer vi tilbake til det samme stedet der 3 veier møtes. Men da har vi gått den siste veien og og vi kan ikke forlate stedet uten å gå en av de veiene vi har gått tidligere. Så hvis ikke vi har vært innom alle veiene og avslutter her, har vi et problem.
Hva hvis ikke vi skulle begynne øverst i venstre hjørnet? Tenk at vi starter på et av stedene der tre veier møtes. Vi vil komme tilbake til det og forlate det igjen. Men da kan vi ikke komme tilbake uten å gå en av de veiene vi allerede har gått.
Dette betyr at hvert av stedene der antallet veier er et oddetall, må enten være starten eller slutten av hele ruta. Men dette betyr at vi ikke kan ha flere enn to steder der antall veier er et oddetall.
På bildet har vi åtte steder der antallet er et oddetall, og dermed er det umulig.