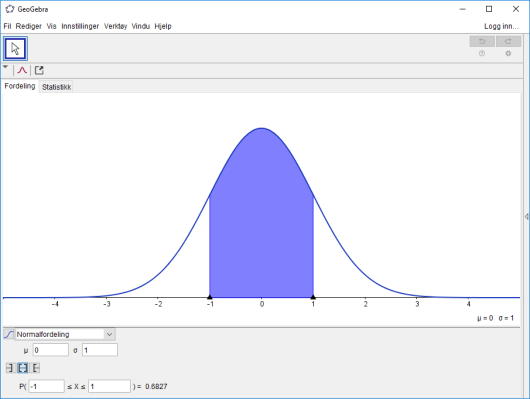
Sannsynlighet
I GeoGebra kan vi også løse sannsynlighetsproblemer og visualisere fordelingene som blir brukt.
GeoGebras sannsynlighetskalkulator er veldig fin for å visualisere sannsynlighet. Vi må passe på å velge riktig sannsynlighetsfordeling, og det gjør vi ved å vite hvilken type oppgave det er vi løser. Dersom oppgaven handler om blodtrykkmålinger, høyder til mennesker og dyr, IQ og mer vil den standarde normalfordelingen passe godt.
Det har seg slik at normalfordelingen er den mest brukte fordelingen fordi den fremkommer oftest i naturen. Vi skal se på et eksempel med binomisk fordeling, og vise at den kan ligne på normalfordelingen.
Eksempel
Milad og Kristine har spurt personer på gata om de er vegetarianere eller ikke. De fant ut at av dem anså seg selv som vegetarianere. De ville gjerne vite hva sannsynligheten for at minst personer er vegetarianer. I tillegg ville de gjerne vite hva sannsynligheten er for at flere enn personer anser seg som vegetarianere. Dette kan vi finne ut av ved å bruke den binomiske fordelingen i sannsynlighetskalkulatoren.
Vi åpner opp sannsynlighetskalkulatoren ved å trykke på den lange vertikale knappen helt til høyre, og velger “Sannsynlighet”. Etter å ha trykket på den knappen får vi dette vinduet opp:
Nå er det slik at normalfordelingen er valgt. Men vi vil ha opp binomisk fordeling. Da trykker vi på der det står “Normalfordeling” og velger “Binomisk fordeling” fra droppvinduet. Og deretter setter vi fordi det var personer som var med i undersøkelsen, og fordi det var som anså seg selv som vegetarianer. Vi får da dette vinduet:
For å finne ut av hva sannsynligheten er for at minst personer er vegetarianer, må vi legge sammen sannsynligheten for at er vegetarianer, er vegetarianer, er vegetarianer osv. helt opp til . Dette kan enkelt gjøres ved å sette inn i verdier der det står ". Vi vil se fra til så vi bytter ut der det står med og får dette:
Sannsynligheten for at minst personer anser seg selv som vegetarianer er eller . Vi vil nå finne ut hva sannsynligheten er for at flere enn personer anser seg som vegetarianer. Her må vi bytte på verdiene i " igjen. Denne gangen bytter vi ut med og med , og ser hva vi får:
Sannsynligheten for at flere enn personer anser seg som vegetarianer er eller .
Her kan man leke seg mer med intervallet. Vi kan til og med finne ut hva sannsynligheten er for at nøyaktig eller nøyaktig personer anser seg som vegetarianere. Vi må bare sette begge verdiene i intervallet til eller .
Normalfordelingen
Vi ser fra eksemplet over at formen på histogrammet likner veldig på formen til normalfordelingen som vi så i det første bildet. Utifra Sentral Grense Teoremet (Central Limit Theorem) vet vi at dersom vi har nok data, så vil fordelingen se mer og mer ut som normalfordelingen. Hvis vi hadde spurt mennesker om de var vegetarianer eller ikke, så hadde den binomiske fordelingen sett enda mer ut som normalfordelingen.
Del på Facebook
Begrep
-
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1. -
Sannsynlighetsteori
Undersøkelser av mulige utfall av gitte begivenheter sammen med deres relative sannsyligheter og forekomster. Det er faktisk betydelig uenighet omkring nøyaktig hva sannsynlighet betyr i praksis. Noen matematikere anser det bare som en komponent i en abstrakt teori, mens andre gir det en tolkning basert på frekvensen av visse utfall.