CAS
Med CAS kan vi faktorisere og forenkle uttrykk, løse likninger og likningssett, finne integraler, derivere uttrykk og mye mer.
CAS blir tilgjengelig gjennom å trykke på knappen helt til høyre i GeoGebra 5, og deretter trykke på knappen “CAS”. Vi skal se på tre eksempler hvor vi viser deg hvordan du kan bruke CAS til å løse vanskelige oppgaver enkelt.
Eksempel, likning
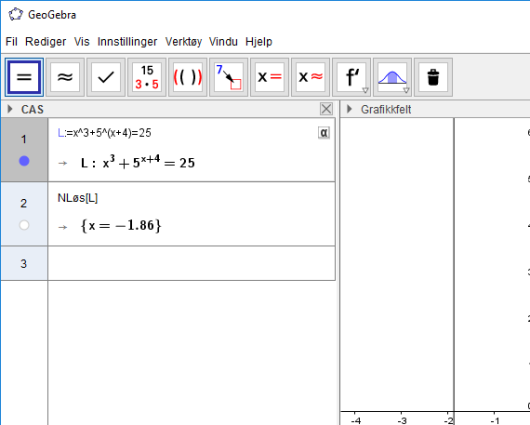
I CAS kan man bruke Løs[ ] for å løse de fleste likninger, men hvis vi vil løse et mer utfordrende likning, må vi bruke NLøs[ ] som løser likningen numerisk. Numeriske metoder er veldig slagkraftige og kan løse likninger som vi ikke har analytiske løsninger på. Likningen er gitt ved:
I det første innskrivingsfeltet i CAS skriver vi inn L:=x^3+5^(x+4)=25, og i det neste skriver vi NLøs[L] og får svaret. Dette kan vi se i bilde under.
Eksempel, likningssett
Vi skal nå sette opp ett likningssett og løse dem med CAS. Likningssettet er gitt under:
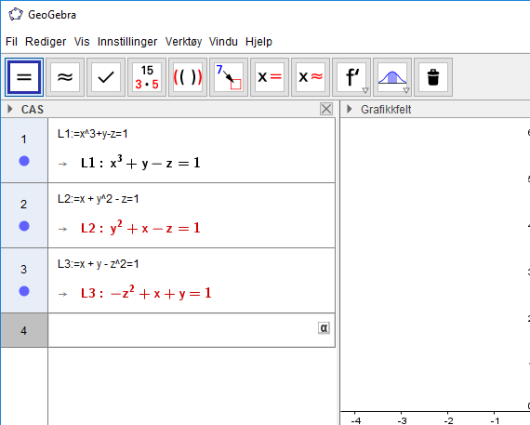
Dette er et likningssett som er vanskelig å løse for hånd hvis ikke man tyr til å gjette på verdier som kan passe inn i likningssettet. Vi bruker heller CAS til å løse likningssettet. I det første, andre og tredje innskrivingsfeltet skriver vi inn L1:=x^2+y-z=1, L2:=x+y^2-z=1 og L3:=x+y-z^2=1. Vi ser under hvordan det skal se ut:
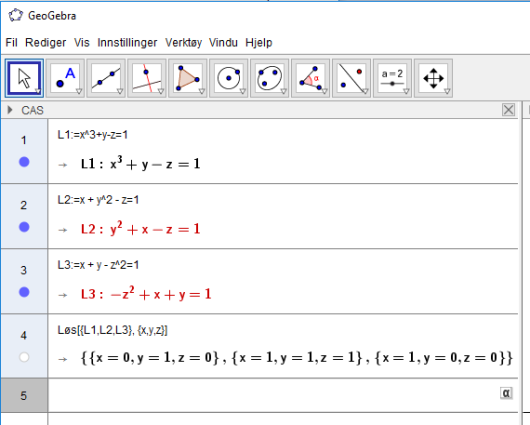
Nå vil vi løse likningssettet, og inn i det fjerde CAS innskrivingsfeltet skriver vi Løs[{L1,L2,L3},{x,y,z}]. Da sier vi til CAS at vi vil løse tre likninger og at variablene er , og . Vi får da dette svaret:
Selv om likningssettet så veldig ille ut, var det ikke noe problem å løse det i CAS.
Eksempel, derivasjon
Med CAS kan vi derivere nesten alle typer funksjoner. Ofte kan det være fint å bruke CAS som en sjekk på at man har derivert riktig. Vi har en funksjon under som kan løses for hånd, men det tar lang tid, og vi vil heller løse den med CAS for å spare tid.
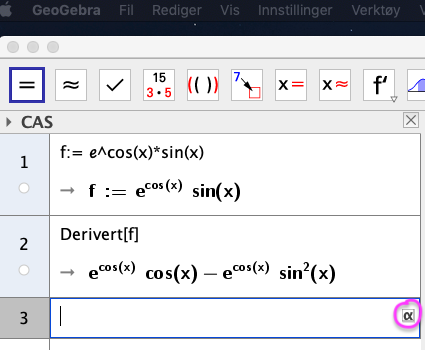
I det første CAS innskrivingsfeltet skriver vi f:=sin(x)*e^(cos(x)). Husk å bruke "" fra symboler du finner ved å trykke på -knappen til høyre i innskrivingsfeltet. I det andre innskrivingssfeltet skriver vi Derivert[f]. Vi får da det følgende svaret:
Så fort går det å derivere med CAS!
Eksempel, integral
Vi kan også integrere funksjoner med CAS. Det er ikke alltid vi kan løse det ubestemte integralet, men som oftest klarer CAS å gi oss det bestemte integralet innenfor ett eller annet intervall. Vi skal se på hvordan vi kan finne det ubestemte og det bestemte integralet for funksjonen under ved å bruke CAS. Funksjonen er ikke vanskelig å integrere for hånd, men det kan ta lang tid.
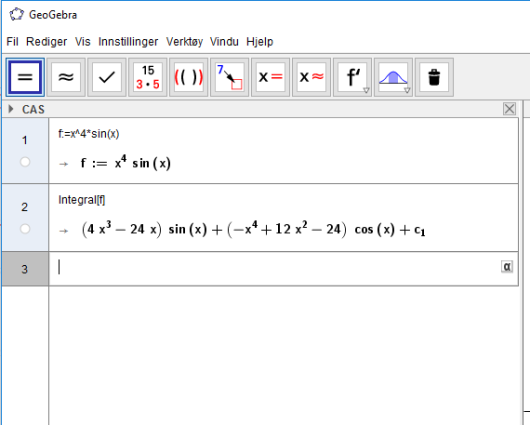
Vi finner det ubestemte integralet først. I det første innskrivingsfeltet skriver vi f:=x^4*sin(x), og i det andre innskrivingsfeltet skriver vi Integral[f]. Vi får da følgende svar:
Det ubestemte integralet kan vi enten finne numerisk eller symbolsk. Hvis man ikke får noe svar ved å bruke den symbolske måten, så er det bare å trykke på den andre knappen fra venstre med bilde av et . Da vil CAS prøve å løse integralet på nytt numerisk. Vi ser nå på funksjonen under:
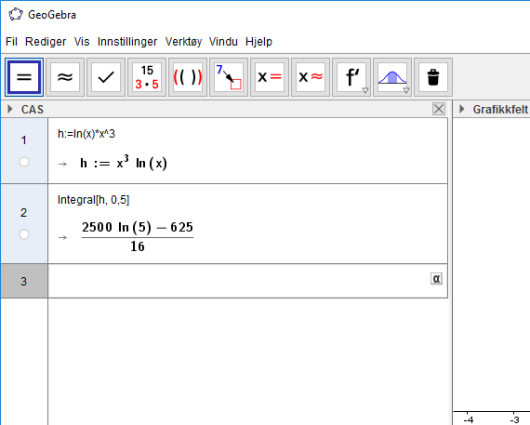
Vi skal finne det bestemte integralet fra til . I det første innskrivingsfeltet skriver vi h:=x^4*ln(x), og i det andre innskrivingsesfeltet skriver vi Integral[h, 0, 5]. Vi får da følgende svar:
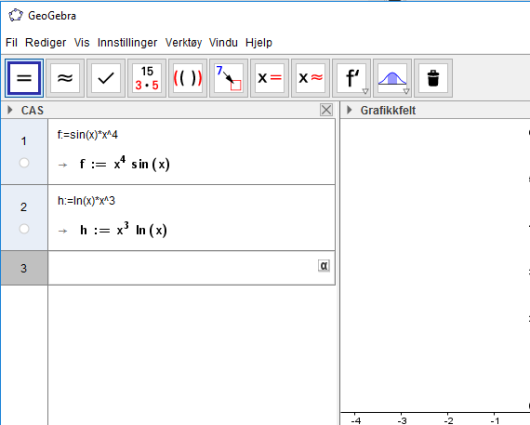
Til slutt vil vi gjøre en siste ting, og det er å finne det bestemte integralet mellom to funksjoner. Vi velger å finne det bestemte integralet mellom funksjonen og for til . Først definerer vi hver av funksjonene som vi gjorde tidligere slik at vi har dette:
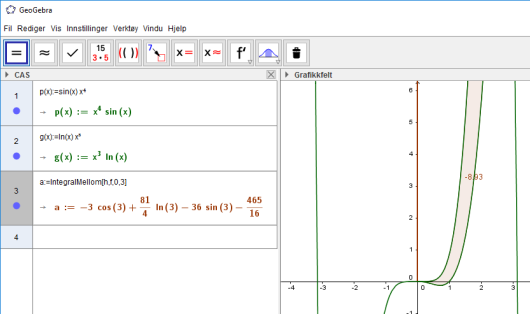
I det tredje CAS innskrivingsfeltet skriver vi IntegralMellom[h, f, 0, 3] og får da svaret. Vi kan også visualisere dette ved å trykke på den lille, hvite sirkelen til venstre, under tallet, tallet og til slutt tallet. Resultatet er da:
Eksempel, Algebra, Faktoriser
Vi har fått et vanskelig algebraisk uttrykk og vil bruke “Faktoriser”-kommandoen.
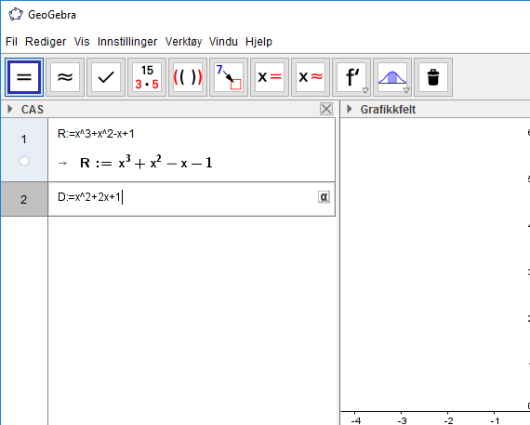
Siden det kan fort ta veldig lang tid for oss å faktorisere, så vil vi bruke CAS. Vi skriver da inn uttrykket i telleren og nevneren hver for seg ved å bruke komandoen, R:=x^3+x^2-x-1 og D:=x^2+2x+1 som vist under:
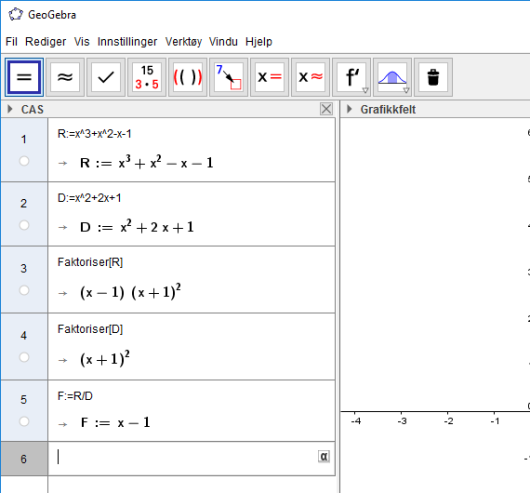
I det tredje og fjerde CAS innskrivingsfeltet skriver vi Faktoriser[R] og Faktoriser[D]. Og i det femte CAS innskrivingsfeltet kan vi skrive F:=R/D og få svaret vårt som vist under:
Eksempel, Algebra, Forenkle
Vi skal nå bruke “Forenkle”-kommandoen til å forenke et algebraisk uttrykk. Vi har det algebraiske uttrykket under:
Først setter vi dette inn i CAS ved å skrive inn kommandoen,
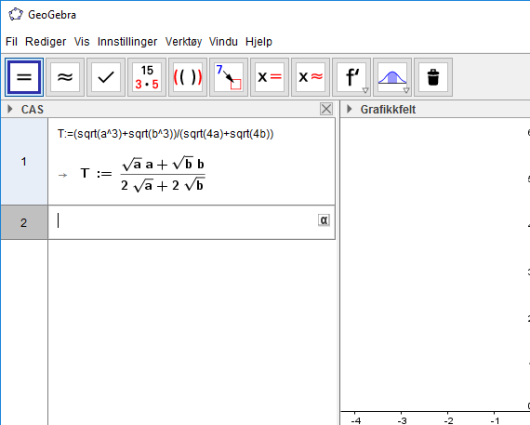
T:=(sqrt(a^3)+sqrt(b^3))/(sqrt(4a)+sqrt(4b)) som vist under.
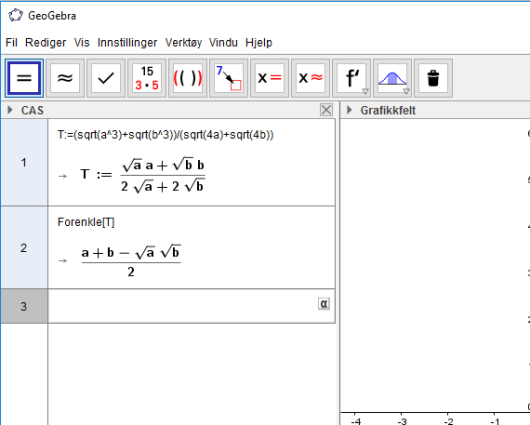
Vi skriver i neste CAS innskrivingsfelt Forenkle[T] og får da svaret:
Lære mer CAS
Vi har nå sett hvor slagkraftig CAS-verktøyet kan være. Beste måten å bli kjent med CAS på er å bruke det. Du kan for eksempel bruke det til å sjekke at du har gjort leksene dine riktig. Istedet for å se i fasit, så kan du sjekke det med CAS og da vil du lære deg CAS veldig fort.
Del på Facebook
Begrep
-
Bestemt integral
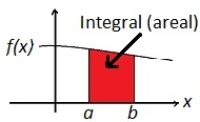
Integralet av en funksjon mellom to grenser.
For en reell kontinuerlig funksjon med positive funksjonsverdier, kan det bestemte integralet tolkes som arealet av området begrenset av grafen til funksjonen, x-aksen og de to grenseverdiene.Det skrives
a og b er grenseverdiene, og f(x) er funksjonen vi integrerer.
-
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
-
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
-
Faktorisering av uttrykk
Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.
Eksempel:
-
Integralregning

Integralregning er forbundet med arealbegrepet. Et areal kan uttrykkes ved et bestemt integral, og det kan beregnes ved integrasjon. Integralet fra a til b av funksjonen f kan tolkes som arealet av det området som begrenses av funksjonens graf, x-aksen og de vertikale linjene x=a og x=b.
-
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
-
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
-
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.