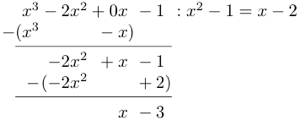Flere eksempler på integrasjon av rasjonale uttrykk
Vi avslutter dette lynkurset med noen videre eksempler på å integrere rasjonale uttrykk.
Eksempel 1
Sørg for å huske hvordan du gjør delbrøkoppspalting før du prøver å løse dette.
Oppgave. Regn ut .
Løsning. Ved delbrøkoppspalting finner vi konstanter , og slik at
Dette gir opphav til et likningssystem der , og er de ukjente. Løser vi dette på vanlig måte, finner vi at , og . Kombinert med teoremet i forrige seksjon får vi fra dette at
, så
,
og med litt opprydding får vi det endelige svaret
.
Eksempel 2
Til slutt gjør vi et eksempel der graden i telleren er større enn graden i nevneren. Da må vi bruke polynomdivisjon for å gjøre graden i telleren mindre enn graden i nevneren. Etter at vi har gjort dette, er resten av regningen som før.
Oppgave.Finn integralet .
Løsning. Her har telleren grad 3, mens nevneren har grad 2. Da er det bare å sette i gang med polynomdivisjon. Vi finner:
Resultatet av divisjonen ble altså , med en rest på . Dette betyr at
slik at
.
Det siste integralet løser vi ved delbrøkoppspating som i de to foregående eksemplene. Ved konjugatsetningen er , og vi finner på vanlig måte oppspaltingen . Dermed er
.
Til slutt setter vi dette inn i likningen vi merket med (1) og får det endelige resultatet:
.
Del på Facebook
Lynkurs 11.-13.trinn
Integrasjon
Består av:
- Ubestemte integraler
- Bestemte integraler
- Halvar forteller om fundamentalteoremet
- Delvis integrasjon
- Integraler som kan løses ved delvis integrasjon
- Integrasjon ved substitusjon
- Flere eksempler på substitusjon
- Integrasjon av rasjonale uttrykk
- Flere eksempler på integrasjon av rasjonale uttrykk
- Halvar utleder formler for volum til kuler og kjegler
- Halvar viser integrasjon av potensfunksjoner
- Halvar viser integrasjon av trigonometriske funksjoner
- Volum av et omdreiningslegeme