Rette linjer (lineære funksjoner)
Lineær funksjon er det matematiske navnet på en rett linje. Når tegneprogrammer som Photoshop vil lagre en rett linje lagres den i bakgrunnen som en lineær funksjon.
I forrige seksjon så vi at en funksjon der variabelen er i første potens blir en rett linje. En lineær funksjon er en funksjon som kan skrives som , der og er konstante tall, mens er variabelen. Vi kaller dette noen ganger for en førstegradslikning fordi den ukjente er i første potens. Alle rette linjer i koordinatsystemer kan skrives som lineære funksjoner. Vi skal starte med noen eksempler.
MatRIC: Linjer i planet
Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC
Grafen til en førstegradslikning
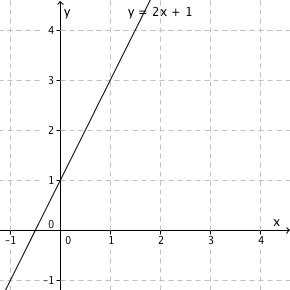
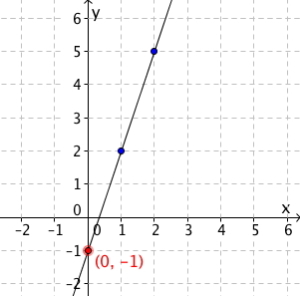
Et eksempel på en lineær funksjon er . Når vi tegner denne lager vi en linje som går gjennom alle punktene som passer i denne likningen. Ett eksempel på et slikt tallpar er og . På tegningen til venstre kan du selv sjekke at dette punktet (og kanskje noen andre du regner ut selv) ligger på linja.
Grafen til
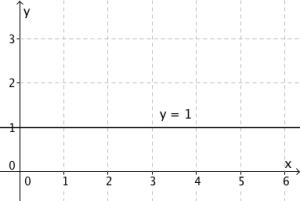
Hvis er det viktig å ikke bli forvirret grafen er fortsatt en rett linje. Siden er 0 blir , og -leddet er altså borte. Det betyr at uavhengig av hvilken verdi av vi velger får vi samme verdi av , og dermed er grafen en flat rett linje. Til venstre har vi tegnet grafen for .
Grafen til bestemmes av og
Ved å se på konstantene og kan man si mye om en lineær funksjon også uten å tegne den. Tallet står ved , og avgjør hvor bratt funksjonen er, mens tallet flytter linja oppover eller nedover i koordinatsystemet.
stigningstall
Tallet kalles stigningstallet til linjen.
Når stigningstallet er negativt, synker linjen når vi beveger oss mot høyre langs -aksen.
Når stigningstallet er positivt, vokser linjen når vi beveger oss mot høyre langs -aksen.
I er stigningstallet . Det betyr at når vi går et steg til høyre langs -aksen, stiger grafen med 2 oppover på -aksen. Sammenlikn med grafen og sjekk at dette stemmer!
konstantledd
Tallet kalles konstantleddet og forteller oss hvor linjen krysser -aksen.
Linjen krysser -aksen når . I er , og det betyr at funksjonsverdien når grafen krysser -aksen er . Sjekk at dette stemmer med begge de to figurene over.
Et eksempel
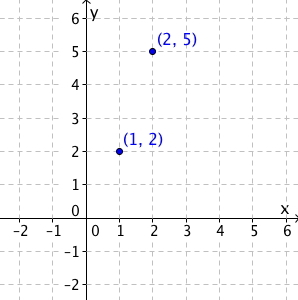
Anta at punktene og ligger på grafen til en lineær funksjon. Vi vil tegne grafen og finne den lineære funksjonen som representerer denne rette linja.
| Først markerer vi punktene: | |
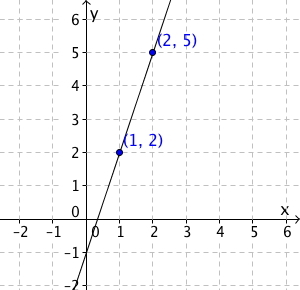
| Og så trekker vi linja: |
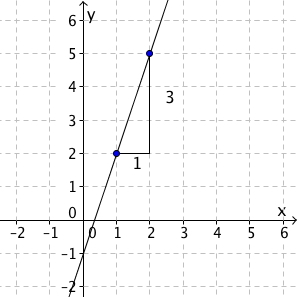
For å finne funksjonen må vi finne stigningstallet og punktet der linjen krysser -aksen. Stigningstallet finner vi ved å se hvor mye vokser når vi øker med 1. De to punktene forteller oss at når øker med 1 øker med 3. Dette betyr at stigningstallet er lik 3.
Konstantleddet finner vi ved å se hvor linjen krysser -aksen. Der er -verdien -1, og som vi forklarte over betyr dette at . Vi har dermed funnet ut at funksjonsuttrykket er .
| Stigningstall: |
|
| Konstantledd: |
|
Et tips: Er du usikker på om du har funnet riktig uttrykk? Sett inn for -verdiene fra de to punktene som ligger på grafen og se når du regner ut om du får de to tilhørende -verdiene.
Del på Facebook
Lynkurs, 8.-10.trinn
Funksjoner (del I)
Består av:
- Hva er en funksjon?
- Koordinatsystem
- Fra en funksjon til en graf
- Rette linjer (lineære funksjoner)
- Proporsjonalitet
- Fra en graf til en funksjon
- Andregradsfunksjoner
- Funksjonsgrafer for andregradsfunksjoner
- Hvorfor ser grafen ut som den gjør?
- Inger Christin forteller om funksjoner.
- Test deg selv i lineære funksjoner!
- Test deg selv i funksjoner!
Begrep
-
Andreakse
Den vertikale/loddrette aksen i et koordinatsystem. Kalles også y-aksen.
-
Førsteakse

Den horisontale/vannrette aksen i et koordinatsystem. Kalles også for x-akse.
-
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
-
Koordinat
Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.
Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.
Se Koordinatsystem
-
Koordinatsystem
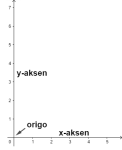
Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
-
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
-
x-akse
Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse. -
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.