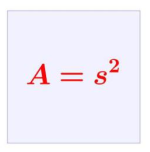Kvadratrøtter
Hva er en kvadratrot?
Tenk på et kvadrat med areal . Arealformelen til et kvadrat med sider av lengde , er
opphøyd i annen potens. Dette gir nettopp arealet i :
Siden , forstår vi at kvadratet har sidelengde . Det positive tallet som multiplisert med seg selv gir , kaller vi kvadratroten av . Vi skriver
.
Vi ser at sidelengden er gitt som kvadratroten av arealet:
, når .
| Definisjon |
| Anta at . Da er (kvadratrota av ) det positive tallet som opphøyd i andre potens er lik . |
Definisjonen legger dermed to krav på kvadratrota av . For det første er og . Med ord betyr dette at kvadratroten til et tall multiplisert med seg selv er lik tallet under kvadratroten. Det andre kravet er at kvadratroten til tallet må være større eller lik 0. Nå skal vi se et eksempel på hva dette medfører.
Eksempel 1.
Finn kvadratroten av .
Nå er og vi får .
Vi ser at resultatet oppfyller kravene i definisjonen, siden og . Vi vet at også
.
Vi kaller likevel ikke for kvadratroten av . Det negative tallet oppfyller ikke definisjonen av en kvadratrot, siden .
Legg ellers merke til at vi kun har definert kvadratrota av tall som er større enn eller lik null Vi kan ikke finne kvadratrøtter av negative tall, fordi ingen reelle tall multiplisert med seg selv gir et negativt produkt.
Eksempel 2.
Løs likningen .
Vi legger til på begge sider av likhetstegnet og trekker sammen like ledd:
Vi ser at er en løsning. Men også . Begge verdiene for stemmer i likningen, og dermed er både og løsninger av denne.
Hvis vi fortsetter å løse likningen skritt for skritt, ville vi ha tatt kvadratroten på begge sider og skrevet følgende
På denne måten vil vi få begge løsningene, fordi står for og .
.
Vi bruker tegnet for å markere de to løsningene.
Likningen har løsningene , som er en kortere måte å skrive og .
Del på Facebook
Lynkurs, 8.-10.trinn
Potenser
Består av:
- Potenser med samme grunntall
- Null og negative tall som eksponenter
- Potenser med brøk som grunntall
- Et produkt eller en potens som grunntall
- Oppsummering av regneregler for potenser
- Inger Christin forteller om potensregler
- Kvadratrøtter
- Kubikkrøtter
- n-te røtter
- Sammenhengen mellom røtter og potenser
- Solsystem og bakterieutvikling - potenser i praksis
- Test deg selv i potenser!
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Brøk
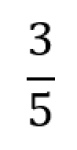
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
-
Kvadrat
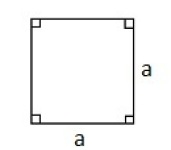
En firkant der alle sider er like lange og alle vinkler 90°.
-
Kvadratrot
Kvadratrot har symbolet .
Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.
Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi . Det skrives .
-
Kvadrattall
Et kvadrattall er det positive heltallet som vi får når et heltall multipliserers med seg selv.
Eksempel: 25 er et kvadrattall, fordi
-
Kvotient
Resultatet av en divisjon kalles en kvotient.
Eksempel: , her er 4 en kvotient.
-
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
-
Likhetstegn
Likhetsteget har symbolet "".
Likhetstegnet forteller at det som står til venstre for likhetstegnet har samme verdi som det som står til høyre.
Eksempel:
-
Naturlige tall
De positive heltallene 1, 2, 3, 4...
Mengden av naturlige tall angis med symbolet .
Hvis 0 skal være med i mengden bruker vi symbolet .
-
Negative tall
Tall som er mindre enn null, kalles negative tall. Vi viser at tallet er negativt ved å sette — foran tallet.
Eksempel: , som leses minus tre.
-
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.Eksempel : . Tallet 7 er nevneren.
-
Positive tall
Tall som er større enn null kalles positive tall.
Eksempel: 1, 78, 435.
-
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel: -
Produkt
Produkt er et resultat av en multiplikasjon.
Eksempel: 2 · 7 = 14
14 er produktet, mens 2 og 7 kalles faktorer. -
Reelle tall
Tall som kan markeres på en tallinje. Mengden av reelle tall er ℝ.
Eksempel: Alle heltall, alle rasjonale tall og alle irrasjonale tall.
-
Rot
Se Kvadratrot