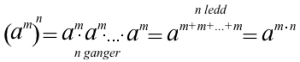www.matematikk.org
LærerstudenterLærerstudenter

Et produkt eller en potens som grunntall

Hva gjør vi når grunntallet er et produkt? Hvordan kan en potens være et grunntall?

Et produkt som grunntall

Hva skjer når grunntallet i en potens er et

Produkt

Produktet er et resultat av en multiplikasjon.

Eksempel : 2·7=14

14 er produktet, mens 2 og 7 kalles faktorer.

produkt
? Hvilke regneregler gjelder her?

Eksempel

Vi starter med produktet 4⋅3, og ser på potensen (4⋅3)3.
(4⋅3)3=4⋅34⋅34⋅3=4⋅3⋅4⋅3⋅4⋅3   
Vi skriver faktorene slik at like faktorer kommer etter hverandre og skriver disse som potenser.

4⋅3⋅4⋅3⋅4⋅3=4⋅4⋅4⋅3⋅3⋅3=43⋅33

 

Det blir akkurat på samme måte for et tilfeldig produkt a⋅b opphøyd i en vilkårlig potens n. Vi får

(a⋅b)n=a⋅b⋅a⋅b⋅...⋅a⋅b

Vi skriver

Faktor

Når tall multipliseres, kalles tallene faktorer. Resultatet kalles et produkt. Eksempel: 5 · 3 = 15. 5 og 3 er faktorer. Tallet 15 er produktet, og vi kan si at produktet består av faktorene 5 og 3.

faktorene
i en rekkefølge slik at de like faktorene kommer rett etter hverandre.

a⋅b⋅a⋅b⋅...⋅a⋅b=a⋅a⋅...⋅a⋅b⋅b⋅...⋅b  (n a-er etterfulgt av n  b-er)

Det siste uttrykket er jo nettopp an⋅bn.

Regel

Produkt av to tall opphøyd i en potens, er lik produktet av faktorene opphøyd i samme potens.

 (a⋅b)n=an⋅bn 



Regelen kan naturligvis utvides direkte til produkt av tre eller flere tall opphøyd i en potens.

Potens som et grunntall

Kan vi virkelig ha en potens i en potens? Hvorfor ikke? Så la oss se på et eksempel.

Eksempel


La oss opphøye potensen 23 i andre potens. Vi får

(23)2=23⋅23  

Husk at når vi multipliserer to potenser med samme grunntall, beholder vi grunntallet og legger sammen eksponentene. Vi bruker denne regelen og får

23⋅23=23+3=26  

Vi vet at 6=3⋅2 og da er

 26=22⋅3 

Men dette betyr at

(23)2=23⋅2
 

Hvis en potens am opphøyes i en ny potens n, får vi følgende

a er opphøyd i m og hele uttrykket er opphøyd i n. Dette er lik a opphøyd i m multiplisert med seg selv n ganger. Dette igjen er lik a opphøyd i (m + m + ... + m) der det er n ledd i parentesen. Dette igjen er lik a opphøyd i (m multiplisert med n).

Regel

Når vi har en potens som grunntall og opphøyer denne i en ny potens må eksponentene multipliseres.

 (am)n=amn 


Av dette kan vi også trekke ut at (am)n=(an)m.

Publisert: 26.07.2013 Endret: 13.10.2014

Lynkurs, 8.-10.trinn

Potenser

Består av:

Begrep

  • Addisjon

    Synonymt med å "legge til", "plusse på".
    Regneoperasjonen 5 + 7 = 12 kalles en addisjon.
    Tallene 5 og 7 kalles ledd, og resultatet kalles en sum.
    Mellom leddene skrives plusstegn (+).

  • Faktor

    Når tall multipliseres, kalles tallene faktorer. Resultatet kalles et produkt. Eksempel: 5 · 3 = 15. 5 og 3 er faktorer. Tallet 15 er produktet, og vi kan si at produktet består av faktorene 5 og 3.

  • Grunntall

    En potens består av et grunntall og en eksponent.
    Eksempel: 4 · 4 · 4 kan skrives som 4³ .
    3-tallet forteller hvor mange ganger 4 her skal stå som faktor. 4 er her grunntallet og 3 er eksponenten i potensen.

  • Multiplikasjon

    Å multiplisere er det samme som å addere samme tall flere ganger. Ofte kalt "ganging". Et av tallene i multiplikasjonen forteller hvilket tall som skal adderes. Det andre tallet forteller hvor mange ganger det skal adderes.

    Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.

    Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
    Mellom faktorene skrives multiplikasjonstegn (·).

    Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.

    Eksempel: 3 · 4 = 12 og 4 · 3 = 12

  • Naturlige tall

    Tallene 0,1,2,3,... De naturlige tallene danner grunnlag for alle andre vanlige tall (hele tall, rasjonale tall, reelle tall, komplekse tall) ved at disse kan konstrueres ut fra de naturlige tallene ved matematiske prosesser. Mengden av naturlige tall er ℕ.

  • Potens

    En potens er et produkt der alle faktorene er like.

    Eksempel:
    4 · 4 · 4 kan skrives som 4³ .
    3-tallet forteller hvor mange ganger 4 her skal stå som faktor. 4 er her grunntallet og 3 er eksponenten i potensen.

    Generelt:
    bª betyr et produkt med a stykker faktorer som alle er lik b.
    Slik:
    b · b · b · b · b ………·b (b er faktor a ganger).

  • Produkt

    Produktet er et resultat av en multiplikasjon.

    Eksempel : 2·7=14

    14 er produktet, mens 2 og 7 kalles faktorer.