Én, mange eller ingen løsninger?
Hvor mange løsninger kan et lineært likningssystem ha?
Et lineært likningssystem har ikke alltid nøyaktig én løsning. Vi skal se nå på tre eksempler som viser likningssystemer med uendelig mange løsninger, ingen løsninger og nøyaktig en løsning.
A) Uendelig mange løsninger
Eksempel
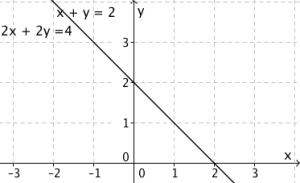
Hvis vi multipliserer alle ledd i med 2, får vi nøyaktig likning . Dette betyr at dette er et likningssett med to like likninger. Hvis vi tegner grafen til likningene i et koordinatsystem, ser vi at vi tegner en og samme linje to ganger.
Grafene ligger oppå hverandre. Punktene som passer i likning (1), er de samme punktene som passer i likning (2). Alle punktene som linjen består av tilfredsstiller kravene til likningene. Dermed har vi uendelig mange løsninger som alle må tilfredsstille .
B) Ingen løsninger
Eksempel
|
|
Hvis du multipliserer venstresiden i likning med 2, får du nøyaktig det samme som venstresiden i likning . Derimot blir ikke høyresidene like ved den samme multiplikasjonen. Her får vi en motsigelse. kan ikke både være 4 og 6. Av dette kan vi si at likningssettet ikke har en løsning. |
||||||||||||||
|
Vi bruker eliminasjonsmetoden for å løse likningssettet. Her ser du også at likningssett har ingen løsninger. |
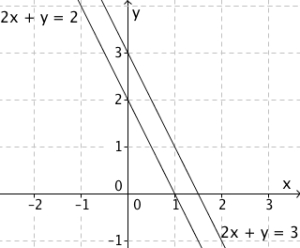
I koordinatsystemet ser vi at grafene er to parallelle linjer. Disse to linjene vil aldri møtes. Likningssettet har ingen løsning.
C) Nøyaktig en løsning
Eksempel:
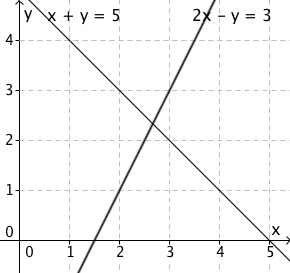
Likningene i likningssystemet er ikke mistenkelig like hverken på høyresiden eller på venstresiden av likhetstegnet. Når vi tegner grafene til likningene i et koordinatsystem, får vi to rette linjer som krysser hverandre i ett punkt . Dette er den entydige løsningen til dette likningssystemet. Her har vi valgt å løse likningen grafisk.
Del på Facebook
Lynkurs, 8.-10.trinn
Likninger
Består av:
- Hva er en likning?
- Førstegradslikninger
- Løs en førstegradslikning!
- Andregradslikninger
- Løs en andregradslikning.
- Karoline løser andregradslikninger.
- Likningssystemer
- Grafisk løsning av likningssett
- Prøve- og feilemetoden
- Addisjonsmetoden
- Substitusjonsmetoden
- Inger Christin forteller om likningssystemer.
- Én, mange eller ingen løsninger?
- Inger Christin løser likninger.
- Test deg selv i 1.gradslikninger!
- Test deg selv i likninger!
Begrep
-
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
-
Kartesisk koordinatsystem
Et koordinatsystem der aksene står vinkelrett på hverandre.
-
Koordinatsystem
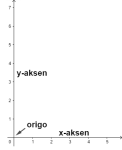
Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
-
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
-
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
-
Lineære ligninger
Ligninger der alle de ukjente opptrer i første grad.
Eksempel:
-
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
-
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·). -
Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.
Tegnet som forteller at to linjer er parallelle:Eksempel: , leses "linja g er parallell med linja f".
-
Punkt
I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.