Kuleformet akvarium fylles med vann

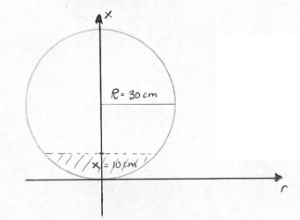
Her er en oppgave jeg lurer på om dere kan hjelpe meg med: Et kuleformet akvarium med radius 30 cm fylles med vann, 50${cm}^3$ pr. sekund. Hvor hurtig stiger vannet i akvariet ved det tidspunkt da vanndybden (midt i akvariet) er 10 cm?

Det finnes en egen formel for volumet av et kulesegment (det skraverte området på bildet). $V\left(x\right)=\pi x^2(R-\frac{x}{3})$

Løsningsforslag:
(går på bruk av kjerneregel)

Vi vet at endringen av vannmengden inne i akvariet 

$\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}$

er oppgitt 50 cm³/s.

Slik jeg forstår oppgaven skal vi finne 

$\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}$

(ved x = 10 cm)

Vi kan sette opp følgende

 $\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}=\frac{\mathrm{\Delta }V}{\mathrm{\Delta }x}\cdot \frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}$

$\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}=\frac{\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}}{\frac{\mathrm{\Delta }V}{\mathrm{\Delta }x}}=\frac{50{cm}^3/s}{V^{\prime }(x=10)}=\frac{1{cm}^3/s}{10\cdot \pi {cm}^2}\approx 0,032cm/s$

Jeg har utelatt noen mellomregninger som jeg anbefaler at du ser på selv, og så er det en ting til; - den deriverte av en funksjon gir deg alltid endringen av det du ser på i utgangspunktet (med hensyn på det du har som variabel).