Formel for areal av trekant og beregninger i likesidet trekant

Kan du hjelpe meg?

Oppgave 1)
For å finne areal til en vilkårlig trekant med grunnlinje g og høyde h bruker vi formelen $\frac{gh}{2}$. Vis/forklar at denne formelen er riktig.

Oppgave 2)
Konstruer en likesidet trekant ABC med sidelinje lik 5 cm. Konstruer høyden fra punkt C til siden AB. Dette punktet kan kalles D.
a) Hvilken lengde har CD? Bruk linjal.
b) Regn ut arealet av trekanten ABC.
c) Kan du finne lengden til CD uten å bruke linjal?

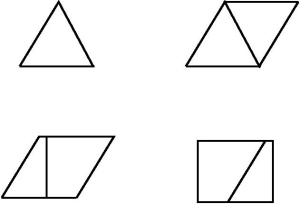
1) Se den første figuren. Du kan lage parallellogrammer fra to sider i en trekant ved å speile i den tredje siden. Arealet til trekanten blir da halve arealet til parallellogrammet. Parallellogrammer har areal grunnlinje ganger høyde: kutt parallellogrammet langs en høyde, og føy sammen igjen på den andre siden. Da har du et rektangel med lengde grunnlinjen, og bredde lik høyden. Trekanten har altså areal halvparten av grunnlinje ganger høyde: $A=\frac{gh}{2}$.

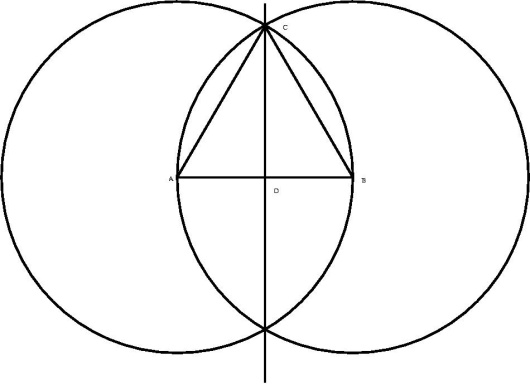
2) Se den andre figuren. Tegn et linjestykke, merk av punkt A og punkt B i avstand 5 cm. Passeråpning 5 cm, merk av to kryssende buer, en fra A og en fra B. De krysser i C. Du har nå en likesidet trekant. Vanligvis feller man ned en normal ved å bruke en bue og merke av to punkter, men her kan vi bruke samme passeråpning som gir punktene A og B. D, foten for høyden, er midtpunktet: to kryssende buer fra A og B nedover, og trekk linjen med C.

a) Dette bør du gjøre selv. (4,3 cm)
b) $A=\frac{gh}{2}=\frac{5 cm\cdot 4,3 cm}{2}\approx 10,8 {cm}^2$.
c) Trekanten ACD er en 30-60-90-trekant. Vi kan derfor bruke Pytagoras: I en rettvinklet trekant er summen av kvadratene på sidene inn mot den rette vinkelen (katetene) lik kvadratet på siden som strekker over den rette vinkelen (hypotenus). Vi regner uten benevning:

${AC}^2= {AD}^2+{CD}^2$

$5^2={\left(\frac{5}{2}\right)}^2+{CD}^2$

$5^2-{\left(\frac{5}{2}\right)}^2={CD}^2$

${\left(\frac{5}{2}\right)}^2(2^2-1)={CD}^2$

${\left(\frac{5}{2}\right)}^2\cdot 3={CD}^2$

$CD=\frac{5}{2}\sqrt{3}\approx 4,3$

Og dermed er CD cirka 4,3 cm.