Andre kvadratsetning
Spørsmål:
Kari, 17
Hei!
Jeg forstår ikke hvorfor den andre kvadratsetningen er . Kan du forklare dette for meg?
Svar:
Hei, Kari!
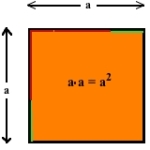
For å forstå hvorfor den andre kvadratsetningen er slik den er, skal vi se på arealet til et kvadrat med sidelengde a.
| 1) Se på et kvadrat med sidelengde . Arealet av et vilkårlig kvadrat er sidelengde multiplisert med sidelengde. Dette gir oss arealet lik . | |
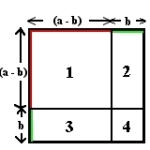
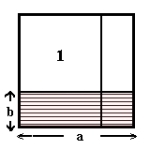
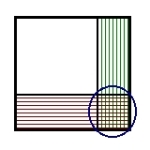
| 2) Del opp kvadratet på samme måte som det er vist på bildet - sidelengden av det minste kvadratet er og det gir at sidelengden til det større kvadratet (1) er . | |
|
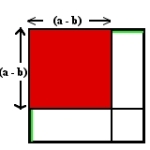
3) Arealet av kvadratet (1) med sidelengder er
|
Nå er det to alternative måte å fortsette beviset for andre kvadratsetningen.
ALTERNATIV 1:
a) Aarealet av kvadrat (1) er det samme som å trekke fra det største kvadratet (med sidelengde a) arealet av rektanglene (2 og 3) og det lille kvadratet (4).
|
||||
|
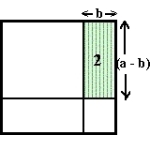
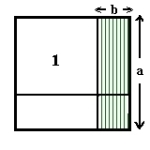
Areal av rektangel (2)
|
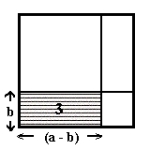
Areal av rektangel (3)
|
Arealet av kvadrat (4)
|
||
c) Areal av kvadrat (1) er
Under 3) fant vi at kvadrat (1) har areal
Dette betyr at disse utrykkene må være like og vi har at
ALTERNATIV 2:
| Arealet av kvadrat (1) fås ved å dele opp det størte kvadratet (med side lengde ) i et stort kvadrat (1) og to rektangler. | ||
|
Areal av rektangel (2)
|
Areal av rektangel (3)
|
Areal av kvadratet (4)
|
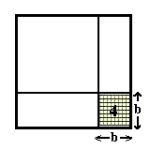
d) Arealet av kvadratet (1) er det samme som å trekke fra det største kvadratet (med sidelengde a) arealet av disse to rektangler, men husk å legge til arelaet av det lille kvadratet (innringet område på bildet).
Grunnen til dette er at det lille kvadratet er en del av begge rektanglene og når vi trekker fra areal av rektanglene, vil vi trekke fra dette arealet to ganger i stedet for én.
e) Arealet av kvadratet (1) er
I følge 3) har kvadrat (1) areal lik , og i foregående punkt fikk vi et annet uttrykk for arealet på det samme kvadratet. Dette betyr at disse utrykkene må være like og vi har at
Vennlig hilsen,
Oraklet
Ofte stilte spørsmål
- Regning (tall, prosent, brøk, gange)
- Algebra (likninger, faktorisering)
- Funksjonsdrøfting
- Bevis
- Geometri (passer og linjal, areal og omkrets)
- Måling
- Sannsynlighet
- Statistikk
- Tallteori
- Matematikkens historie
- Formelsamling
- Generelt om matematikk og orakelet
- Spørsmål om spill
Vi har samlet på noen av svarene som orakelet har gitt. Spørsmål og svar finner du under følgende temaer: