Høyden til stigen
Spørsmål:
Rino, 24
En kasse på 1x1 meter står inntil en vegg, og en stige på 10 meter står lent inntil veggen slik at den berører kassens øvre hjørne. Hvor langt opp på veggen når stigen?
Svar:
Hei, Rino!
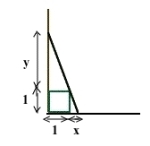
Først tegner vi en figur og markerer de kjente størrelsene:
Vi ser at vi har en stor rettvinklet trekant der der den ene kateten er meter lang. Den andre kateten er meter, mens hypotenusen er 10 meter. Nå kan vi bruke Pytagoras' læresetning og sette opp regnestykket:
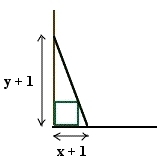
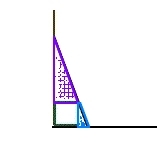
Vi kan se på figuren en gang til og finne to formlike trekanter.
Den største trekanten har kateter og 1, mens den minste har 1 og . Ved å bruke formlikheten av disse, kan vi sette opp en likning til:
Vi skriver uttrykket om og får
Nå har vi to likninger med to ukjente som vi kan løse ved hjelp av substitusjonsmetoden (innsettingsmetoden), sett inn for x i likning (1) uttrykket fra likning (2):
Nå lar vi
og vi får en annengradslikning med z som den ukjente:
Vi bruker løsningsformelen for andregradsllikning og får at
undefined0
Siden vi er ute etter lengder, trenger vi kun bry oss om den positive verdien til , dvs.
Husk at
slik at vi har en likning med den ukjente
Dette er en andregradslikning med den ukjente . Vi bruker løsningsformelen for andregradslikninger og får følgende to løsninger:
Husk at
slik at vi får to løsninger for ,
.
Vennlig hilsen,
Oraklet
Ofte stilte spørsmål
- Regning (tall, prosent, brøk, gange)
- Algebra (likninger, faktorisering)
- Funksjonsdrøfting
- Bevis
- Geometri (passer og linjal, areal og omkrets)
- Måling
- Sannsynlighet
- Statistikk
- Tallteori
- Matematikkens historie
- Formelsamling
- Generelt om matematikk og orakelet
- Spørsmål om spill
Vi har samlet på noen av svarene som orakelet har gitt. Spørsmål og svar finner du under følgende temaer: