Trekant med 45 graders vinkel
Spørsmål:
Aleksander, 14
Konstruer en trekant ABC hvor AB = 6 cm, og vinkel B = vinkel C = 45º.
Svar:
Hei, Aleksander!
Her skal vi ta det skritt for skritt.
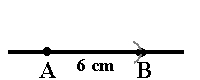
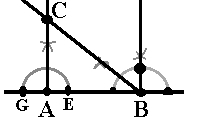
- AB = 6 cm: Først tegner du en linje der du merker av punktet A. Bruk linjalen og ta 6 cm som avstand ipassseren. Sett passerspissen i A og slå en bue på linjen til venstre for punktet A. Punktet der buen og linjen krysser hverandre er punktet B. Linjen AB kaller vi grunnlinjen til trekanten ABC.
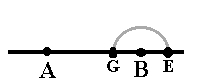
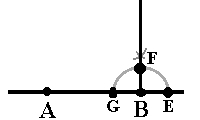
- : Sett passerspissen i punktet B og tegn en halvsirkel. Punktet der halvsirkelen krysser linjen til venstre for B, kaller du G og punktet til høyre kaller du E.
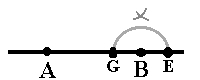
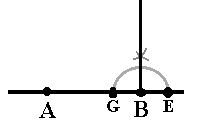
Sett paserspissen i punktet G og slå en liten bue. Behold passeren slik den er, sett passerspissen i punktet E og slå en bue til. Disse to buene skal krysse hverandre. (Hvis de ikke gjør det, må du ta større avstand i passeren og prøve på nytt.) Nå tegner du en linje som går gjennom punktet B og dette krysset, det vil si du feller ned normalen i B. Nå er vinkelen B lik 90°.
| Halvering av 180o vinkel | Normalen på B |
Men ifølge oppgaven skal vinkelen B være 45°. Da må vi halvere vinkelen B vi har konstruert.
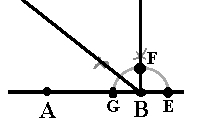
- Halvering av 90° vinkel: Punktet der halvsirkelen og normalen i B krysser hverandre, kaller du F. Sett passerspissen i punktet F og slå en bue. Behold passeren slik den er, sett den i punktet G og slå en bue til. Disse to buene skal krysse hverandre. Tegn en linje som går gjennom B og krysset. Nå er vinkelen B lik 45°.
| Punkt F | Vinkelen GBF er halvert |
Punktene G, E og F er bare hjelpepunkter slik at du kan fjerne dem og bruke dem som hjelpepunkter under neste konstruksjon. Et eller annet sted på den siste linjen du tegnet, ligger punktet C. For å finne ut hvor på denne linjen C ligger, må vi ha litt mer informasjon.
Vi vet at vinkelen C er lik 45°, men vi får ikke konstruert den så lenge vi ikke vet hvor punktet C befinner seg. Men hva mer vet vi? Jo, summen av vinklene i en trekant er 180° og vi vet at vinkelen B og vinkelen C er 45°. Dette gir oss at vinkelen A er
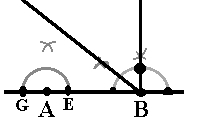
- Da kan vi konstruere vinkelen A. Vi gjør dette på tilsvarende måte som vi gjorde med vinkelen B. Først tegner vi en halvsirkel og merker av punktene G og E. Sett passerspissen i G og slå en bue. Behold passeren slik den er, sett passerspissen i punktet E og slå en bue til. Buene krysser hverandre. Tegn en linje som går gjennom punktet A og dette krysset.
| Halvering av 180o vinkel | Normalen på A |
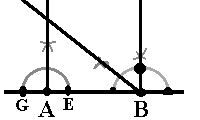
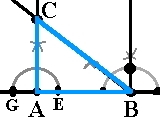
Normalen på A krysser vinkelbeinet til vinkelen B. Punktet der linjene krysser hverandre, er punktet C.
| Det tredje og siste hjørnet i trekanten | Trekanten ABC |
Vennlig hilsen,
Oraklet
Ofte stilte spørsmål
- Regning (tall, prosent, brøk, gange)
- Algebra (likninger, faktorisering)
- Funksjonsdrøfting
- Bevis
- Geometri (passer og linjal, areal og omkrets)
- Måling
- Sannsynlighet
- Statistikk
- Tallteori
- Matematikkens historie
- Formelsamling
- Generelt om matematikk og orakelet
- Spørsmål om spill
Vi har samlet på noen av svarene som orakelet har gitt. Spørsmål og svar finner du under følgende temaer: