Dihedralvinkel, normalvektor til plan fra vinkler med horisontalplanet

Skal finne vinkelen mellom en plate og horisontalplanet. Har to målte vinkelverdier, disse er målt normalt på hverandre(nord-syd og øst-vest). Hvordan summere disse til en samlet verdi?

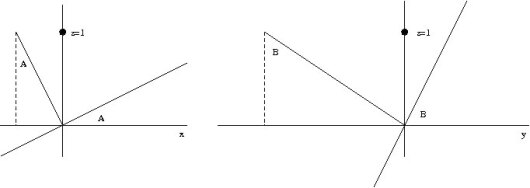
Vinkelen mellom planene kalles dihedralvinkelen og er lik vinkelen mellom normalene. Dine vinkler gir oss normalvektoren til platen: La origo ligge på snittlinjen,$x$-aksen være parallell øst-vest og$y$-aksen være parallell nord-syd. Jeg kaller vinklene dine for$A$ og$B$. For horisontalplanet kan vi velge normalvektoren$(0,0,1)$. Vi velger oss en normalvektor med$z$-koordinat 1. Se på situasjonen i$xz$- og$yz$-planene i figuren.

Vi kjenner altså lengden av hosliggende katet (stiplet), 1, og vi vil ha lengden av motstående katet. Den motstående til A delt på 1 må være lik tangens til A, så den motstående til A er tangens til A, og samme for B. Normalvektoren er altså

$(-\tan (A),-\tan (B),1)$. Vi kaller dihedralvinkelen for$\phi$, den er da vinkelen mellom de to normalvektorene, og sammenhengen mellom vinkelen mellom to vektorer og vektorene er kjent:

$\cos \left(\phi \right)=\frac{(0,0,1)\cdot (-\tan (A),-\tan (B),1)}{1\cdot \sqrt{1+{\tan \left(A\right)}^2+{\tan \left(B\right)}^2}}$.

$\phi ={\cos }^{-1}\left(\frac{1}{\sqrt{1+{\tan }^2\left(A\right)+{\tan }^2\left(B\right)}}\right)$.

Dette er den generelle formelen når du har to målte vinkler,$A$ og$B$, som står normalt på hverandre.

Eksempler:$A=B=0$ gir dihedralvinkel 0.

$A={30}^{\circ }$,$B={60}^{\circ }$ gir dihedralvinkel cirka 61º.