Parallelle tangenter

En funksjon $f$ er gitt ved $f\left(x\right)=x^3+x^2$.

a) Finn likningen for tangenten i punktet $(1,f(1\left)\right)$.

b) Grafen til $f$ har en tangent som er parallell med tangenten i $(1,f(1\left)\right)$. Finn likningen for denne tangenten.

Jeg trenger svar på disse spørsmålene... Hjelp meg, Orakel.

Funksjonen $f$ tar et tall til et tall: $x\mapsto x^3+x^2$. Grafen $y=f\left(x\right)$ er de parene av tall $(x,y)$ som henger sammen som punkt og verdi for $f$.

$(1,f\left(1\right))=(1,1^3+1^2)=(1,2)$ er et punkt på grafen til $f$.

a) Grafene til funksjoner på formen $l\left(x\right)=ax+b$ gir linjer. (Sammen med $x=c$, som er linjer som ikke er graf til noen funksjon, er dette alle linjene.) Tangenten til grafen til $f$ i et punkt er en linje gjennom punktet som har stigningstall $a$ lik den deriverte i punktet:

$\frac{df}{dx}\left(x\right)=3x^2+2x$,

$\frac{df}{dx}\left(1\right)=3\cdot 1^2+2\cdot 1=5$.

Vi bruker dermed $a=5$: $l\left(x\right)=5x+b$. Det andre kravet er at $l$ går gjennom punktet $(1,2)$, så vi krever $l\left(1\right)=2$.

$l\left(1\right)=5\cdot 1+b=5+b=2$,

$b=2-5=-3$.

Tangenten til $f$ i $(1,2)$ er $y=5x-3$.

b) Linjer er parallelle om de har samme stigningstall. Vi må derfor løse ligningen

$\frac{df}{dx}\left(x\right)=5$: $3x^2+2x=5$,

$x^2+\frac{2}{3}x=\frac{5}{3}$,

$x^2+\frac{2}{3}x+\frac{1}{9}=\frac{5}{3}+\frac{1}{9}$,

${(x+\frac{1}{3})}^2=\frac{16}{9}$,

som gir oss $x+\frac{1}{3}=\frac{4}{3}$ eller $x+\frac{1}{3}=-\frac{4}{3}$, det vil si $x=1$ eller $x=-\frac{5}{3}$. Det første svaret vet vi allerede om, vi skal dermed ha det andre. Den parallelle tangenten er altså gjennom punktet $(-\frac{5}{3},f(-\frac{5}{3}))=(-\frac{5}{3},-\frac{50}{27})$. Da får vi

$m\left(x\right)=5x+b$,

$m(-\frac{5}{3})=-\frac{25}{3}+b=-\frac{50}{27}$,

$b=\frac{175}{27}$.

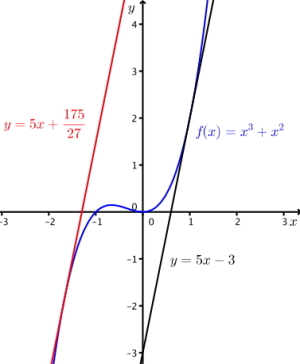
Den parallelle tangenten er $y=5x+\frac{175}{27}$. Se figuren under.