Funksjoner, lineære og kvadratiske, proporsjonalitet og grafer

Hva er proporsjonalitet? Hva er en kvadratisk funksjon? Hva er omvendt proporsjonalitet? Hvordan regner vi med funksjonsutrykk? Hvilket ledd i funksjonsutrykket forteller om grafens stigning? Hva er $a$- og $b$-leddet når du ser på en graf?

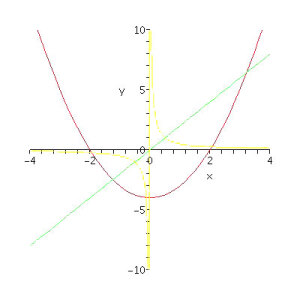
Bildet under viser forskjellige eksempler, se nederst. Proporsjonalitet er en sterk sammenheng mellom to størrelser som varierer. $x$ og $y$ er proporsjonale om $y=kx$, der $k$ ikke varierer. $y$ er null om $x$ er null,$y$ øker om $x$ øker. $y=kx$ er en linje og du kan tenke på den som grafen til funksjonen $f\left(x\right)=kx$, se den grønne grafen i vedlegget: $y=2x$.

En kvadratisk funksjon er en funksjon på formen $f\left(x\right)=a{x}^2+bx+c$ der $a$,$b$ og $c$ er konstanter. Grafen er oftest en parabel, se den røde grafen i vedlegget, $y=x^2-4$.

Omvendt proporsjonalitet er en sterk sammenheng mellom to størrelser som varierer.$x$ og$y$ er omvendt proporsjonale om $y=\frac{k}{x}$, der$k$ er konstant. $y$ øker om $x$ minker og omvendt. $y=\frac{k}{x}$ er en hyperbel, og du kan tenke på den som grafen til funksjonen $f\left(x\right)=\frac{k}{x}$. Se den gule grafen i vedlegget: $y=\frac{1}{2x}$.

Funksjonsutrykket er regneregelen du setter$x$ inn i for å få $f\left(x\right)$. Det er ikke noe mystisk, regnereglene er de vanlige. Har vi noen $x$ og tilhørende $f\left(x\right)$ og vet hvilken type funksjon det er (for eksempel lineær eller kvadratisk) kan vi finne utrykket ved å bestemme konstantene til funksjonen ved å sette opp ligninger, en for hvert punkt. Vi trenger like mange ligninger som ukjente.

For det siste antar jeg at du snakker om $f\left(x\right)=ax+b$, der $a$ og $b$ ikke varierer. Grafen $y=f\left(x\right)$ til en slik lineær funksjon er en linje. Her er $a$ stigningstallet, og sier hvor mye grafen stiger eller synker i forhold til punktet du kom fra når du går 1 til høyre (altså i positiv retning). $b$ er skjæringspunktet med y-aksen:

$f\left(0\right)=a\cdot 0+b=b$, så funksjonen går gjennom punktet $(0,b)$, som ligger både på y-aksen og grafen.