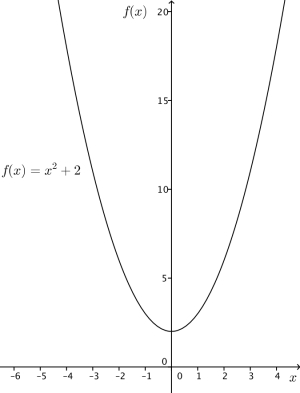
Grafen til x^2+2
Spørsmål:
Astrid, 16
Har litt problemer med ()-,()-,()- og ()-reglene og funksjonen
.
Hvordan blir tabellen til dette funksjonsuttrykket ovenfor når jeg skal bruke disse-verdiene: -4, -3, -2, -1, 0, 1, 2, 3, 4? Hva blir da?
Svar:
Hei, Astrid!
.
.
er alltid større enn eller lik null for reelle tall. Grunnen til det er at enten er et ikkenegativt tall, og pluss ganger pluss blir pluss, eller så er et negativt tall, og minus ganger minus blir også pluss. Så de to "kryssreglene" kommer aldri i spill her.
Funksjonen din, er dermed alltid større enn eller lik. Grafen til funksjonen din er punktene med koordinater slik at, altså.
For eksempel i -4, får vi utregningen, og i -3 får vi, og så videre. Tabellen blir
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
| 18 | 11 | 6 | 3 | 2 | 3 | 6 | 11 | 18 |
Vi ser at funksjonen er symmetrisk, altså at like langt fra 0 i begge retninger har den samme verdi.
Vennlig hilsen,
Oraklet
Ofte stilte spørsmål
- Regning (tall, prosent, brøk, gange)
- Algebra (likninger, faktorisering)
- Funksjonsdrøfting
- Bevis
- Geometri (passer og linjal, areal og omkrets)
- Måling
- Sannsynlighet
- Statistikk
- Tallteori
- Matematikkens historie
- Formelsamling
- Generelt om matematikk og orakelet
- Spørsmål om spill
Vi har samlet på noen av svarene som orakelet har gitt. Spørsmål og svar finner du under følgende temaer: