Hva er integralregning?

Hei, lurte på om dere kunne forklare litt om integralregning: Hvordan regne på det, sammenheng med derivasjon, og så videre?

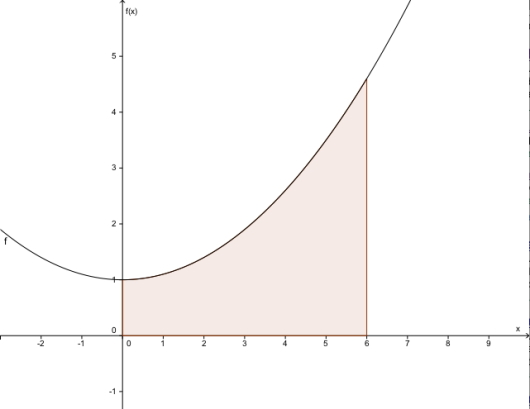
Enkel forklaring: Å integrere er det samme som å anti-derivere (å finne ut av hvilken funksjon du deriverte til å begynne med). Når du integrerer finner du f.eks arealet under en graf, for eksempel det skraverte området i bildet under. Hvis en funksjon er f og den antideriverte er $F$ er arealet under funksjonen mellom punktene $a$ og $b$ gitt ved $F\left(a\right)-F\left(b\right)$, forutsatt at den er positiv (Om den ikke er det kan man dele opp området i flere mindre).

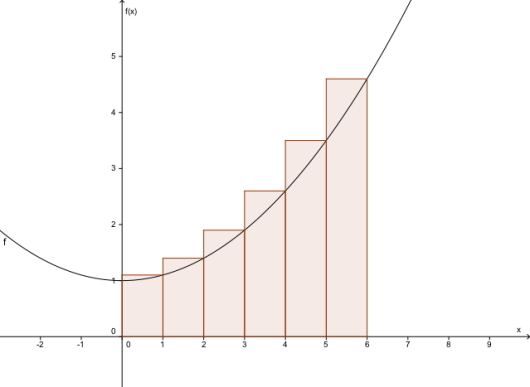
Den vanskeligere, men mer presise, forklaringen er at integralet er en slags sum. Integraltegnet er rett og slett en utstrukket S (for sum). Det man gjør for å finne integralet er å velge en (liten) avstand $dx$ i $x$-retning. Poenget er at om man holder $dx$ konstant vil $f\left(x\right)\cdot dx$ gi deg arealet av en tynn boks med høyde $f\left(x\right)$ og grunnlinje $dx$. Om du lager sånne bokser regelmessig bortover får du en slags trappesum, illustrert her:

Hvilken ende vi velger å la boksen møte funksjonen i er ikke så viktig. Som du ser er dette en tilnærming til arealet, om enn upresis. Det man gjør matematisk nå er å la $dx$ gå mot null, altså la boksene bli 'uendelig smale'. Da får man etterhvert en nøyaktig arealsum (Om funksjonen er positiv). Om vi starter i punktet $x=a$ og slutter i $x=b$ kaller vi denne grensesummen for

${\int }_a^{b}f\left(x\right)dx$. Dette er altså matematisk notasjon for 'arealet under funksjonen $f$ fra punktet $a$ til punktet $b$'. Om funksjonen er negativ vil du få et negativt areal, så det du gjør når funksjonen skifter fortegn er å dele opp området i flere områder der funksjonen er enten bare positiv eller bare negativ, regne alle de for seg (og ta absoluttverdi av negative arealer) og til slutt summere dem for å få hele arealet.

Om vi lar den øvre grensen variere kaller vi integralet ubestemt, og da er det en funksjon av denne.

Hvis

$F\left(x\right)={\int }_a^{x}f\left(t\right)dt$

er

$\frac{d}{dx}F\left(x\right)=f\left(x\right)$.

Videre er ${\int }_a^{b}f\left(t\right)dt=F\left(b\right)-F\left(a\right)$.

Generelt finnes det mange antideriverte av en funksjon, siden den deriverte av en konstant er null kan du legge til en konstant og få en annen antiderivert. Å bestemme konstanten som skal legges til vil kreve mer informasjon om den antideriverte enn at den skal være en antiderivert, for eksempel kan man vite dens funksjonsverdi i et punkt. Om vi bare ønsker en eller annen antiderivert skriver vi ofte integrasjonstegnet helt uten grenser og legger til en ubestemt konstant C i svaret, siden det har mange løsninger.

For å klare å regne med integraler må du kjenne til en del deriverte slik at du kan bruke den kunnskapen "baklengs" for å få antideriverte. Vi vet for eksempel at

$\frac{d}{dx}{x}^n=n{x}^{n-1}$, og da kan vi se av det at

$\int n{x}^{n-1}dx=x^n+C$, der vi legger til en konstant på grunn av det nevnte over. Om vi her lar $m=n-1$ får vi regelen

$\int x^{m}dx=\frac{x^{m+1}}{m+1}+C$. Denne gir ikke mening om $m=-1$, som tilsvarer å prøve å finne integralet av $\frac{1}{x}$. Da må vi bruke at vi vet at $\frac{d}{dx}\ln \left(x\right)=\frac{1}{x}$, og dermed er

$\int x^{-1}dx=\ln \left(x\right)+C$.

Med denne informasjonen kan du integrere vanlige polynomer, men man kan også sette sammen antideriverte etter regler som stammer fra baklengs bruk av for eksempel produktregelen, eller kjerneregelen.

Det er generelt mange trekk i dette spillet man bør kjenne til: Polynomer, brøker av polynomer, elementærfunksjoner som eksponentialfunksjonen og de trigonometriske er blant de funksjonene vi kan integrere eksakt. Når man setter dem sammen kan man få løst integraler for ganske mange forskjellige funksjoner.

For funksjoner vi ikke klarer å integrere direkte kan vi gå tilbake til definisjonen av integralet og få tilnærminger ved å ikke la boksbredden gå mot null, men heller la den være liten, og summere arealene (tilpasninger av denne metoden brukes ofte på datamaskiner for å gjøre integrasjonen numerisk).