Radius når kordlengde og høyden er kjent
Spørsmål:
Simen, 25
Lurer på hva formelen er for å finne radiusen på en sirkel når mann bare har en liten del/bue av sirkelen. Kordelengden er 135 cm og høyden fra korde til buen er 20 cm.
På forhånd takk:-)
Svar:
Hei, Simen!
Ved hjelp av blant annet formlike trekanter har man bevist flere ulike setninger for korder. En av disse er:
Hvis to korder i en sirkel krysser hverandre, er produktet av lengdene av segmentene (linjestykkene) på den ene korden lik produktet av lengdene av segmentene på den andre korden.
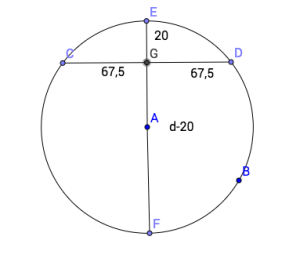
Hvis to korder krysser hverandre og i dette tilfellet er også diameteren en korde, er produktet av linjestykkene og til korden lik produktet av og til korden (se bildet). Ved hjelp av dette kan du lage en formel selv.
Siden vi vet at produktene er like, har vi at
Deretter kan vi finne diameteren ved å sette inn for alle linjestykkene.
Siden vi har fått vite at er en høyde fra korden, så betyr det at korden blir delt opp i to like store deler og derfor er .
Fra oppgaveteksten får vi vite at . Siden vi vet at er diameter, da har vi at
Deretter setter vi inn alle segmentene inn i formelen og får:
Radius vil da være
Det finnes også en generell formel, hvor h er høyden og R er radius:
Det er nok best å bruke det faktumet at produktet av segmentene er like, fordi den generelle formelen kan være vanskelig å huske og bruke.
Vennlig hilsen,
Oraklet
Ofte stilte spørsmål
- Regning (tall, prosent, brøk, gange)
- Algebra (likninger, faktorisering)
- Funksjonsdrøfting
- Bevis
- Geometri (passer og linjal, areal og omkrets)
- Måling
- Sannsynlighet
- Statistikk
- Tallteori
- Matematikkens historie
- Formelsamling
- Generelt om matematikk og orakelet
- Spørsmål om spill
Vi har samlet på noen av svarene som orakelet har gitt. Spørsmål og svar finner du under følgende temaer: