Koordinater til skjæringspunkt mellom diagonaler i en firkant

Tema: Vektorer mellom punkter. Å bestemme punkter.

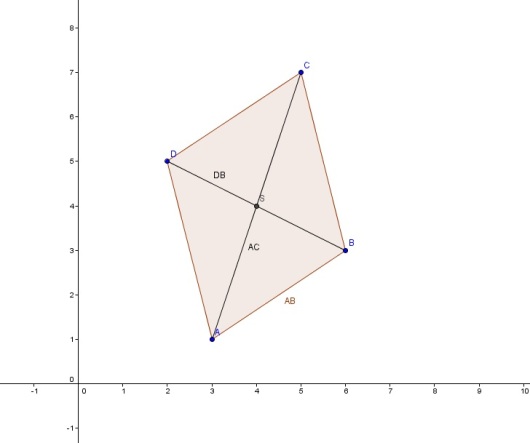
Tegn punktene A(3,1) B(6,3) C(5,7) og D (2,5) Trekk opp firkanten ABCD. Bestem vektorene AB, AC og BD. Tegn inn skjæringspunktet S mellom diagonalene AC og BD. Forklar at det finnes tall, x og y , slik at AS= xAC og AS= AB + y BD
Så kommer spørsmålet om å sette opp en vektorlikning og bestemme x og y. Deretter finne koordinatene til S. Dette får jeg ikke til.
Ønsker å se utregning på dette :-)

Tegning av firkanten ABCD med skjæringspunktet S mellom diagonalene AC og BD.

Punktene er A(3,1), B(6,3), C(5,7) og D(2,5).

For å finne vektorene $\overrightarrow{AB}$, $\overrightarrow{AC}$, og $\overrightarrow{BD}$, bruker vi en formel for dette:

Hvis A og B er punkter, er vektoren $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$. I vårt tilfelle er A = (3,1) og B = (6,3), så $\overrightarrow{OA}=[3,1]$ og $\overrightarrow{OB}=[6,3]$.

 $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=[6,3]-[3,1]=[6-3,3-1]=[3,2]$ 

På samme måte finner vi $\overrightarrow{AC}$ og $\overrightarrow{BD}$:

 $\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}=[2,6]$ 

 $\overrightarrow{BD}=\overrightarrow{OD}-\overrightarrow{OB}=[-4,2]$ 

Ved å se på tegningen så er det klart at vektoren $\overrightarrow{AC}$ er en forlengelse av vektoren $\overrightarrow{AS}$, siden S er et punkt på linjen. Det betyr at $\overrightarrow{AC}$ og $\overrightarrow{AS}$ har samme retning, dvs at de er parallelle. Det betyr at vi kan skalere $\overrightarrow{AC}$ ned til $\overrightarrow{AS}$ med et tall. Med andre ord finnes et tall $x$ slik at $\overrightarrow{AS}=x\cdot \overrightarrow{AC}$

Med samme argumentasjon som over ser vi at det må finnes et tall $y$ slik at $\overrightarrow{BS}=y\cdot \overrightarrow{BD}$. Med regler for vektoraddisjon er $\overrightarrow{AS}=\overrightarrow{AB}+\overrightarrow{BS}$. Så setter vi inn for $\overrightarrow{BS}$, og får likningen $\overrightarrow{AS}=\overrightarrow{AB}+y\cdot \overrightarrow{BD}$ .

Ved å sette den første likningen inn for $\overrightarrow{AS}$ i den andre likningen, ender vi opp med likningen

 $x\cdot \overrightarrow{AC}=\overrightarrow{AB}+y\cdot \overrightarrow{BD}$ 

Nå setter vi inn for koordinatene vi kjenner til $\overrightarrow{AC}$, $\overrightarrow{AB}$ og $\overrightarrow{BD}$:

 $x\cdot [2,6]=[3,2]+y\cdot [-4,2]$ 

 Dette gir oss likningene

 $2x=3-4y$ 

 $6x=2+2y$ 

Vi bruker den første likningen til å isolere $x$:

 $x=\frac{3-4y}{2}=\frac{3}{2}-2y$ 

Så setter vi dette inn i den andre likningen:

 $6(\frac{3}{2}-2y)=2+2y$ 

 $6\cdot \frac{3}{2}-6\cdot 2y=2+2y$ 

 $9-12y=2+2y$ 

 $9-2=2y+12y$ 

 $7=14y$ 

 $y=\frac{7}{14}=\frac{1}{2}$ 

Dette gir oss at

 $x=\frac{3}{2}-2y=\frac{3}{2}-2\cdot \frac{1}{2}=\frac{3}{2}-1=\frac{1}{2}$ 

Nå finner vi $\overrightarrow{AS}$ ved å sette inn for $x$:

 $\overrightarrow{AS}=x\cdot \overrightarrow{AC}=\frac{1}{2}\cdot [2,6]=[\frac{1}{2}\cdot 2,\frac{1}{2}\cdot 6]=[1,3]$ 

Formelen for vektorer og punkter er $\overrightarrow{AS}=\overrightarrow{OS}-\overrightarrow{OA}$. Ved å flytte $\overrightarrow{OA}$ over på den andre siden, får vi $\overrightarrow{OS}=\overrightarrow{AS}+\overrightarrow{OA}$. Så vi setter inn for $\overrightarrow{AS}$ og $\overrightarrow{OA}$:

 $\overrightarrow{OS}=[1,3]+[3,1]=[4,4]$ .

Så koordinatene til S er altså (4,4).