Mia og Marius på Nysgjerrigpers 20-årsfest
Mia og Marius stiller opp på Nysgjerrigpers 20-årsfest. Der utfordrer de Terje til å finne ut i hvilket år bladet Nysgjerrigper var dobbelt så gammelt som spalten til Mia og Marius, og Marianne til å finne det maksimale antall kakestykker ved hjelp av tre rette kutt.
Historien
Hei, så fint at dere kunne komme, sier Terje når han tar imot Mia og Marius.
Søskenparet er invitert i Nysgjerrigpers 20-årsfest.
Klart vi måtte komme, sier Mia, vi har jo hatt egen spalte i bladet siden 2001. Og du var også med da vi startet, men jeg kan ikke huske at du har fått en matematikkoppgave ennå. Det må vi rette på, sier Marius til Terje. I 2010 er bladet Nysgjerrigper 16 år gammelt mens "Mia og Marius-spalten" er ni år gammel.
Oppgave 1:
I hvilket år var bladet Nysgjerrigper dobbelt så gammelt som spalten til Mia og Marius?
Mens Terje tenker så det knaker får Mia og Marius øye på Marianne og Kate som står ved kakebordet. De skynder seg over dit for å slå av en prat.
Så hyggelig å se dere her, sier Marianne. Dere har jo reist verden rundt gjennom spalten i bladet. Hvor skal dere reise nå?
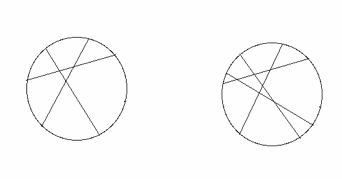
Akkurat nå har vi ingen planer, sier Mia. Vi skal bare kose oss på festen deres. Terje fikk nettopp en oppgave av oss, så da har vi også lyst til å gi dere en. Her er en rund kake. Vanligvis deler vi den i kakestykker som er like store, men nå får dere en oppgave der kakestykkene ikke trenger å ha samme form eller samme størrelse.
Oppgave 2:
Du skal dele en kake med rette kutt fra den ene til den andre siden av kaken. Hvor mange kakestykker kan du maksimalt dele den i med tre kutt? Og hvor mange med fire kutt? NB: Husk at stykkene ikke trenger å ha samme form eller være like store.
Mens Marianne og Kate begynner å snitte i kakene er en hyggelig dame kommet over til Marius. Det er Birgitte, som tegner søskenparet i bladet.
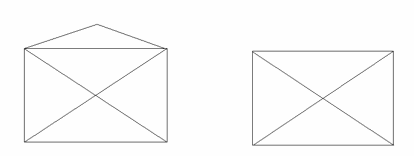
Hyggelig å hilse på deg, svarer Marius. Siden du tegner oss må du få en tegneoppgave. Klarer du å tegne disse to figurene uten å løfte blyanten og uten å tegne samme strek to ganger? Du har lov til å være innom samme punkt flere ganger eller krysse en strek du har tegnet, men altså ikke tegne samme strek to ganger.
Oppgave 3:
Kan du tegne figur A og B uten å løfte blyanten eller tegne samme strek to ganger? (Hvis du mener at det ikke er mulig, prøv å forklare hvorfor.)
Fasit
Oppgave 1
I 2008. Nysgjerrigperbladet er sju år eldre enn spalten til Mia og Marius. Det er derfor kun når spalten er sju år gammel at bladet er dobbelt så gammelt.
Oppgave 2
Hvis du passer på at hvert nye kutt skjærer alle foregående kutt vil du få det maksimale antall biter.
1 kutt: 2 deler
2 kutt: 4 deler
3 kutt: 7 deler
4 kutt: 11 deler
Oppgave 3
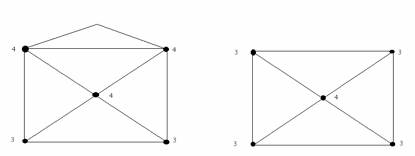
Figur A er mulig, figur B er umulig.
Se på de stedene der flere linjer møtes. Bortsett fra det punktet du starter i og det punktet du slutter i skal du bare besøke de andre punktene. For at det skal gå, må det være et partall streker ut fra de andre punktene (slik at det er like mange veier inn som ut). Det kan altså maksimalt være to punkter med et odde antall linjer. Figuren viser at du kan tegne A, men ikke B.