Mia og Marius i vikingtiden
Mia og Marius er på kulturhistorisk museum for å se på vikingutstillingen. De lærer om vikingenes måleenheter og får se en 1000 år gammel spillterning som ikke har like store sider - hva blir sannsynligheten for å slå en 6'er nå?
Historien
Velkommen til Universitetets kulturhistoriske museum her i Oslo. Så fint at dere ville komme på besøk til oss. Mitt navn er Ingrid, og jeg skal vise dere litt rundt i vikingutstillingen. Men før det skal Svein lære dere litt om veiing i vikingtiden.
Klassen til Mia og Marius er på besøk i Oslo og i dag skal de lære om vikinger.
Vikingene brukte skålvekter når de veide gull- og sølvsmykker, sier Svein. Først legger jeg dette gullsmykket i den ene skåla. Så legger jeg noen vektlodd i den andre skåla. Når vektstanga står vannrett er det like mye i begge skålene. Jeg har tatt med tre slags vektlodd som vikingene brukte. Det største kalte de mark, og det tilsvarer ca. 216 gram. Det nest største var øre, som var ca. 27 gram, og det minste var ertog, som var ca. 9 gram.
Siden du hadde tre av de nest største og to av de minste i vektskåla så betyr vel det at gullsmykket veier 3 øre og 2 ertog, sier Marius.
Oppgave 1
a) Hvor mange ertog er det i en øre? Og hvor mange ertog er det i en mark?
b) Bruk opplysningen til Marius til å finne hvor mye gullsmykket veier målt i gram.
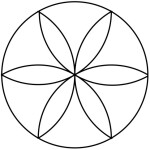
Da kan dere litt om veiing, sier Ingrid. La dere forresten merke til det fine mønsteret i bunnen av vektskålene? Det ser ut som en blomst med 6 blader inne i en sirkel. Vet dere hvordan man kan lage et slikt mønster?
Jeg er ikke sikker, sier Mia, men siden det er en sirkel kan man kanskje bruke en passer.
Det er riktig, sier Ingrid. Først tar dere en passer og tegner en sirkel. Behold den samme åpningen i passeren og sett passerspissen på sirkelperiferien og slå buer inne i sirkelen. Jeg har tatt med noen passere så dere kan prøve.
Oppgave 2
Bruk en passer og tegn mønsteret som er inne i vektskålen (se figur til høyre).
Nå går vi inn i utstillingen, sier Ingrid.
Å, ja, sier Marius, det blir kult. Hadde forresten vikingene noe å leke med?
Jada, de hadde blant annet terninger som de brukte til spill. Her skal dere se noen rare terninger som er over 1000 år gamle. De likner litt på våre terninger, men ser dere noe som er annerledes?
Ja, sier Mia, terningene har ikke like store sider, og de minste sidene har ikke øyne.
Riktig, sier Ingrid. Terningene skulle ikke lande på kortsidene, derfor var de uten øyne.
Ja, og på de fire sidene med øyne er det 3, 4, 5 og 6, sier Marius.
Oppgave 3
a) Hvor stor er sjansen for å slå en 6-er med en slik terning?
b) Hvis du slår to slike terninger, hvilken sum er den mest sannsynlige å få?
(Tips: Sett opp en tabell hvor det vannrett står hva du kan få på den ene terningen og det loddrett står hva du kan få på den andre terningen. Fyll deretter ut hele tabellen)
(Ekstra: Hvis du vil lage en vikingterning så er målene 2,2cm · 22cm · 29cm.)
Fasit
Oppgave 1
a) Antall ertog i en øre er 27:3 = 3.
Antall ertog i en mark er 216:9 = 24.
b) Gullsmykket veier 3·27gram + 2·9gram = 99 gram.
Oppgave 3
a) Siden terningen har fire sider den kan lande på er sjansen for å få en 6-er.
b) Vi kaller terningene A og B og setter opp mulige øyne på de to terningene i en tabell
| A/B | 3 |
4 | 5 | 6 |
| 3 | 6 | 7 | 8 | 9 |
| 4 | 7 | 8 | 9 | 10 |
| 5 | 8 | 9 | 10 | 11 |
| 6 | 9 | 10 | 11 | 12 |
Fra tabellen ser vi at den summen som kan fås på flest måter er 9. Dette kan vi få på 4 måter ut av i alt 16 mulige. Vi ser at det er mest sannsynlig å få 9, og at sannsynligheten for å få det er .