Mia og Marius på utstilling
Mia og Marius drar sammen med kusinene Ella og Alva på Teknisk museum i Oslo der de besøker matematikkdelen av utstillingen Sultans of Science. Her utfordrer de hverandre i det romerske tallsystemet, likninger og geometri.
Historien
- Hei, så hyggelig å treffe dere igjen, sier Mia og Marius i det de kommer inn døra på Teknisk museum i Oslo. Sammen med kusinene Ella og Alva skal de på utstillingen Sultans of Science for å lære om naturvitenskap innen islamsk kultur i middelalderen.
- Vi går til matematikkdelen først, sier Alva.
- Vet dere hva, sier Ella, de tallene vi bruker kalles indisk-arabiske fordi de først ble funnet opp i India. Det var for 2000 år siden. De kom til Bagdad for 1200 siden, og først for ca. 800 år siden lærte europeerne om disse tallene fra handelsmenn og arabiske skrifter.
Ja, sier Mia, og det finnes et 700 år gammelt manuskript fra Norge der de samme tallene beskrives. Det ble eid av Hauk Erlendsson og begynner slik:
Denne kunsten heter algorismus. Indiske menn fant den først og gjorde den med X tegn som blir skrevet slik: 0 9 8 7 6 5 4 3 2 1.
Den nye regnekunsten til inderne kalte Hauk for "algorismus". Hauk forklarer at i den indiske regningen bruker man ti talltegn (10= X med romertall) og han forteller hvordan tegnene ser ut.
Oppgave 1
a) Finn ut hvordan tallene åtte og tjueseks skrives med romertall.
b) Hvorfor tror du at han brukte romertall (X=10) for å fortelle om de nye tallene inderne hadde funnet opp?
Litt lenger inne i utstillingen har Marius kommet over en spennende plakat.
Se her, sier han, det står at araberne også var flinke til å løse likninger. Den best kjente av dem var kanskje Muḥammad ibn Mūsā al-Khwārizmī. Han var tilknyttet noe som het Visdommens hus, opprettet av kalifen i Bagdad rundt år 800.
Ja, sier Mia, han har vi hatt om på skolen. Han skrev en lærebok om hvordan man løste likninger. En metode het al-jabr, som betyr "å gjenoppbygge på den andre siden av likhetstegnet". Det ordet brukes i matematikken over hele verden i dag i ordet algebra.
Oppgave 2
Å løse en likning betyr å finne et skjult eller hemmelig tall. Fra et regnestykke skal du finne et hemmelig tall som gjør at regnestykket blir riktig.
a) Finn det hemmelige tallet (tallet i boksen) når :
b) Finn det ukjente tallet når
For et flott palass, sier alle i kor. Foran dem er et bilde av Alhambra i Granada i Spania. Dekorasjonene i palasset hadde form som rektangler. Alle rektanglene hadde bredde 1, men de kunne ha forskjellig høyde.
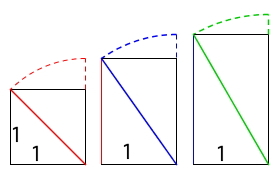
Dette var litt vanskelig, sier Marius. Her står det hvordan man bestemte hvilke høyder man fikk lov å bruke. Diagonalen i et rektangel bestemte høyden i neste rektangel.
Oppgave 3
a) Nedenfor ser du hvordan man fra diagonalen i et rektangel finner høyden i neste rektangel. Studer tegningen og bruk passer og linjal til å tegne de fire første rektanglene.
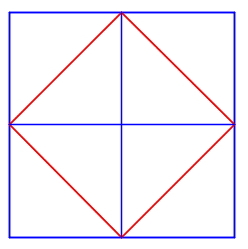
b) Nedenfor ser du en figur med kvadrat i tre størrelser. Sidekantene i de minste kvadratene har lengde 1. Finn arealet til de tre ulike kvadratene i figuren.
Fasit
Oppgave 1
a)
| VIII | 8 |
| XXVI | 26 |
b) Sidene de indiske-arabiske tallene var nye, kjente ingen til dem. Derfor måtte han bruke de gamle tallene som folk kjente, nemlig romertall.
Oppgave 2
a) Tallet er 24 fordi
b) Tallet er 3 fordi
Oppgave 3
a) Hvis du har tegnet veldig nøyaktig blir høyden på det fjerde rektangelet lik 2.
b) Areal av minste kvadrat 1, mellomste kvadrat 2 og største kvadrat 4.
Litt om romertall.
Opp til 100 finnes det egne tegn for 1 (=I), 5 (=V), 10 (=X) og 100 (=C). Et nytt tall blir laget ved å sette talltegnene ved siden av hverandre, med de største talltegnene lengst til venstre,
32 = XXXII. Hvis vi plasserer et talltegn til venstre for et med høyere verdi, må det trekkes fra:
IV = 51 = 4.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| X |
XX |
XXX |
XL |
L |
LX |
LXX |
LXXX |
XC |
C |
Eksempel: LXXXVII = 50 + 10 + 10 + 10 + 1 + 1 = 87