Fraktaler med datamaskin

Ved hjelp av datamaskiner kan man lage fraktale bilder, enten basert på enkel geometri som over, eller gjennom gjentatte beregninger med (relativt) enkle formler.

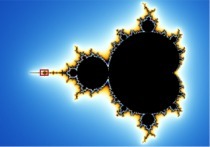
Med en datamaskin kan man også få fram detaljer og på den måten demonstrere egenlikhet i mer komplekse fraktaler, som Mandelbrot mengden (under).

Bildet under til høyre viser det som er i den lille røde firkanten i bildet under til venstre.

Slik kan man fortsette å zoome inn og stadig komme over samme formen.

Ved hjelp av fraktaler kan man lage virkelighetsnære naturbilder, eller man kan bruke fraktalene til å lage rene fantasibilder. En Kochkurve hvor det er tilfeldig hvilken vei spissene peker kan for eksempel danne grunnlaget for en kystlinje, eller en Cantormengde hvor linjestykkene roteres tilfeldig kan danne grunnlag for støv eller skyer.

Hentet fra exoteric.roach.org

Hentet fra exoteric.roach.org

Hentet fra exoteric.roach.org

I det første bildet kjenner vi igjen Mandelbrotmengden, og i det andre er fraktaler brukt til å etterlikne naturen. Det siste bildet er også basert på fraktaler. 

Ved å bruke fraktal grafikk i digitale bilder reduseres datamengden som lagres og man får plass til flere bilder uten å øke lagringsplassen.

Mandelbrotmengden kan knyttes til den tilsynelatende enkle formelen:

$f_c\left(z\right)=z^2+c$

hvor c og z er komplekse tall. Før vi kommer inn på hvordan Mandelbrotmengden oppstår, må vi se nærmere på komplekse tall.