Symmetrier
Kjenner du to jenter som heter ANNE og ANNA? Hva er forskjellen på dem? Annet enn at det er to forskjellige jenter?
Figur 1: Symmetrisk mønster.
Matematisk sett er det en vesentlig forskjell på de to jentenavnene. Navnet ANNA er likt bakfra og forfra, mens ANNE ikke har denne egenskapen. Det matematiske begrepet som vi snakker om her er det vi kaller symmetri. I dagligtale bruker vi ordet symmetrisk om ord som for eksempel ANNA. Det ser symmetrisk ut fordi det er det samme enten vi leser forfra eller bakfra. På samme måte sier vi at et mønster er symmetrisk dersom noe er likt den ene og den andre veien, eller opp og ned slik som mønsteret i figur 1.
Når vi driver med matematikk har begrepet symmetri en bredere mening. Vi snakker ikke bare om at noe er symmetrisk, vi vurderer også hvor symmetrisk det er. Vi stiller oss spørsmålet: Hvilke symmetrier har denne figuren?
La oss gå tilbake til navnene ANNA og ANNE. Navnet ANNE har ingen symmetrier, baklengs blir navnet ENNA, opp ned blir det noe helt annet. Derimot har ANNA én symmetri, nemlig at det kan leses baklengs og fortsatt være det samme navnet. Vi kan ta en kikk på noen av bokstavene våre og se på hvilke symmetrier de har som geometriske figurer.
A, M, T, U, V, W, Y og Å kan leses forfra og bakfra.
C, D og K kan snus opp ned.
F, G, J, L, P, Q, R og Æ har ingen symmetrier.
H, I og X kan snus opp ned og leses bak fram.
N, S, Ø og Z kan dreies 180 grader.
O kan dreies rundt og rundt, leses opp ned og bak fram.
Som vi ser er det nokså ulike grader av symmetrier, fra de som ikke har noen, som for eksempel F, til O, som har flest symmetrier. (I noen skrifttyper blir O-en litt avlang og mister derfor mange av sine symmetrier.) Vi ser også at når vi ser på bokstavene som geometriske objekter så er faktisk ikke ANNA likt forfra og bakfra, rett og slett fordi en N ikke er lik når vi leser den baklengs. Som bokstavkombinasjon, derimot er ANNA symmetrisk. Forskjellene er at i det ene tilfellet ser vi bare på bokstavenes form, i det andre bryr vi oss ikke så mye om bokstavenes form, men mer om hvilke bokstaver som inngår i ordet og i hvilken rekkefølge. Et annet ord av samme type er REKKER.
Men det er ikke bare ord som kan ha en slik bak-fram-egenskap. Også tall kan ha en slik egenskap. Her er det lettere å finne eksempler, det er bare å skrive dem opp, f.eks. 26462. Slike tall har egne navn, de kalles palindrome tall. En liten oppgave: Hvor mange palindrome 1-sifrede tall finnes og hvor mange 2-sifrede tall er palindrome? Og 3-sifrede?
Som vi gjorde med bokstaver kan vi gjøre med tallene: Se bort fra meningen med tallet og se på den utelukkende som en geometrisk figur. Oppgave: Klassifiser tallene fra 0-9 på samme måte som vi gjorde med bokstavene over.
Nå finnes det sikkert mange andre interessante geometriske figurer, ikke bare bokstaver og tall.
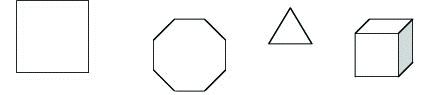
Figur 2: Et lite utvalg symmetriske figurer.
I fiugr 2 ser vi et lite utvalg med litt forskjellige symmetrier. Et kvadrat har fire symmetrier, nemlig vridninger med 90 grader. Åttekanten har på tilsvarende måte åtte symmetrier, mens trekanten har tre. Terningen, eller kuben, er litt verre å vurdere, men vi kan telle dem opp. Vi tenker oss at det står tall på alle sideflatene på terningen. I så fall er det 6 forskjellige tall som kan ligge ned mot bordet. For hvert tall som ligger ned, kan vi ha fire forskjellige tall som peker fram. Det betyr at vi har 6 x 4 = 24 symmetrier. Nå kan det virke som om vi alltid har et endelig antall symmetrier, sånn som 4 eller 6 eller 24, men det er ikke alltid tilfelle slik vi så på bokstaven O tidligere.
Figur 3: Sirkel.
I figur 3 har vi en sirkel. Alle mulige dreininger av denne sirkelen rundt dens sentrum vil gi oss symmetrier. Vi kan kalle en rotasjon med en vinkel v for R(v). Dette er et typisk eksempel på matematikk som språk. R(v) kan vi betrakte som en forkortelse for "rotasjon med en vinkel v". Vinkelen v kan være et hvilket som helst tall mellom 0º og 360º. Det fine, sett fra en matematikers synspunkt, er at hvis vi setter sammen to rotasjoner så får vi en ny rotasjon hvor vinkelen er summen av de to vinklene. Vi kan skrive dette som R(v) x R(w) = R(v+w).
Hittil har vi betraktet mangekantene og sirkelen som tegninger på et ark. La oss nå tenke på dem som egne legemer, ikke bare tegninger:
Figur 4: Tenk på tegningene som egne legemer.
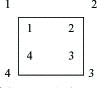
Vi har fortsatt de samme symmetriene som vi hadde over, men i tillegg til rotasjonene, fire for kvadratet og uendelig mange for sirkelen, så kan vi snu figurene opp ned. En måte å framstille dette er å sette nummer på hjørnene på kvadratet og på hjørnene på arket rundt. Så tenker vi oss at vi klipper ut kvadratet, dreier eller snur på kvadratet og legger det ned igjen. Utgangspunktet er altså følgende posisjon
som vi skriver
1 2 3 4
1 2 3 4
altså 1 blir 1, 2 blir 2, osv.
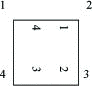
Nå løfter vi ut firkanten, vrir den rundt en gang og legger den ned igjen. Da ser det hele ut som :
som vi skriver
1 2 3 4
4 1 2 3
altså 1 blir 4, 2 blir 1, osv.
Skriveformen under tegningen er litt mer praktisk enn tegningene, og systemet er nokså enkelt. Rett under 1-tallet skriver vi det tallet som er havnet i 1-hjørnet, rett under 2-tallet setter vi det tallet som er i 2-hjørnet, osv. Det som er smart med denne skriveformen er at vi har et system for å sette sammen rotasjoner. Hvis vi roterer videre med 90º vil vi få 4 i øvre høyre hjørne, 3 i øvre venstre hjørne, 1 i nedre høyre hjørne og 2 i nedre venstre hjørne. Dette skriver vi som
1 2 3 4
3 4 1 2
På denne måten kan vi lage et algebraisk system som beskriver symmetriene til en firkant, noe som i utgangspunktet var veldig geometrisk. Dette er en av matematikkens berømte koblinger mellom det abstrakte og det intuitive.
Symmetri er et begrep som brukes i nesten alle deler av matematikk. I denne artikkelen har vi bare så vidt berørt emnet, det er veldig mye vi ikke har kikket innom. Men for den interesserte leser finnes hyllemeter på hyllemeter med litteratur om emnet.
Del på Facebook