Møbiusbånd og kleinflaske
Matematikken kan gi oss mange 'rare' objekter. Møbiusbåndet og kleinflasken er to eksempler på geometriske objekter med bare én side...
Ta et ark og klipp ut en sirkel. Sirkelen har to sider, og vi kan dermed orientere sirkelen. Vi kan for eksempel kalle den ene siden "opp" og den andre siden "ned". Sirkelen har også en rand, og vi kan ikke komme fra den ene siden til den andre uten å passere randen. Tilsvarende skjer når vi klipper ut et rektangel: Vi har to sider og en rand (de fire kantene), og hvis en maur klatrer på rektangelet, må den altså passere randen for å komme fra den ene siden til den andre. Dette er egenskaper som ikke forandres selv om vi for eksempel strekker litt på figurene. Disse egenskapene forandres imidlertid raskt når vi begynner å lime... Den delen av matematikken der man studerer egenskaper ved ulike figurer eller former som ikke forandres selv om vi presser sammen eller strekker på figurene, kalles topologi. Vi skal se at vi får nye topologiske figurer ved hjelp av litt lim.
Hva om vi kan gi mauren noe annet enn rektangelet å gå på, for eksempel en figur med bare én side?
Start med et rektangel (en papirremse). Hvis vi limer sammen to av de motstående endene uten å vri på rektangelet, får vi et armbånd (en sylinder). Hvis vi imidlertid snur den ene enden 180 grader før vi limer sammen endene, så får vi en figur med bare en side:
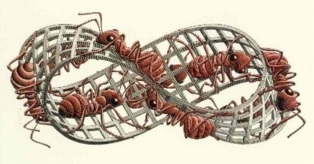
Figur 1: Møbiusbånd
Figuren kalles i dag et møbiusbånd, og den ble oppdaget på midten av 1800-tallet av matematikerne Listing og Møbius, som arbeidet helt uavhengig av hverandre. Båndet kan ikke orienteres: Vi vet ikke hva som er opp eller ned, foran eller bak. Og mauren kan nå plutselig gå rundt på båndet, fra den ene til den andre siden av det gamle rektangelet, uten å passere noen rand! Møbiusbåndet kan jo være kjekt i industrien også: En møbiusviftereim kan man bruke dobbelt så lenge som en vanlig reim. Vi trenger ikke å snu den for å bruke den andre siden...
Mauren kan imidlertid ikke gå i alle retninger på møbiusbåndet uten å støte på en rand, så la oss gå et skritt videre. Kan vi lage en figur med bare én side, uten noen kanter? Det nærmeste vi kommer er å ta en sylinder (åpen i begge ender), strekke den, lage et hull og tre den gjennom seg selv og lime sammen endene. I tegningen nedenfor har vi deformert (strekt ut og presset sammen) sylinderen slik at den ligner en flaske (?):
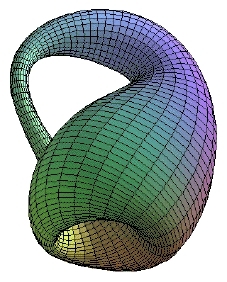
Figur 2: Kleinflaske
Flasken vi får, kalles ofte en kleinflaske, som er oppkalt etter Felix Klein (1849-1925) som forøvrig samarbeidet noe med den norske matematikeren Sophus Lie. Den ekte kleinflasken lever imidlertid i 4 dimensjoner, og vi kan derfor ikke forestille oss hvordan den egentlig ser ut. Men hvis vi ser bort fra sammenbindingen, der halsen tres inn i hullet i flasken, gir tegningen over den riktige formen på en 4-dimensjonal kleinflaske.
Kleinflasken har én side og ingen kanter. Innsiden er utsiden, og den inneholder altså seg selv... Hvis mauren går rundt på en kleinflaske uten å snu seg, kan den plutselig dukke opp på startpunktet bak-fram! Dette er en egenskap ved ikke-orienterbare flater. Møbiusbåndet er byggesteinen for alle slike flater, og i 1882 "lagde" Felix Klein kleinflasken ved å lime sammen to møbiusbånd langs rendene.
Del på Facebook
Begrep
-
Topologi

Et felt i matematikk som studerer egenskaper ved figurer og flater som er uavhengig av kontinuerlige forandringer av størrelse og form.
Illustrasjonen er fra Wikimedia commons.