Fortegnslinja 1
Fortegnslinjer bruker vi for å finne ut når et funksjonsutrykk er positivt og negativt. Vi bruker dem gjerne i funksjonsdrøfting til å se hvordan funksjonen, den deriverte og den dobbeltderiverte oppfører seg.
La være en funksjon. Med fortegnslinja til mener vi en linje der vi markerer hvilke x-verdier som gir positiv, negativ eller null .
Vi har en funksjon
.
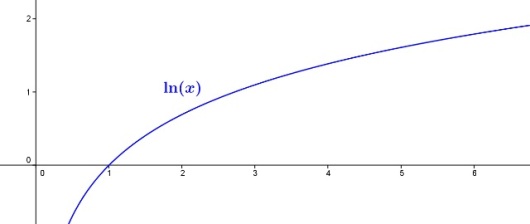
Grafen ser slik ut:
Ut fra grafen ser vi at er negativ for mellom og , positiv for større enn , og har som eneste nullpunkt. Når er mindre enn eller lik , er ikke definert.
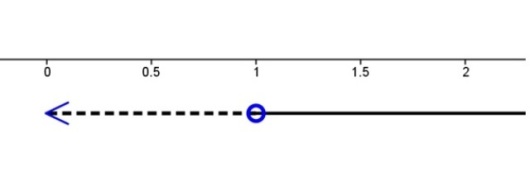
I fortegnslinja markerer vi som følger
der er negativ
der er positiv
der er null
ved for å markere at er definert ned til, men ikke i .
Slik blir den seende ut:
Når vi senere skal tegne fortegnslinja til mer kompliserte funksjoner, kan det være greit å systematisere litt. I boksen under gjennomgår vi punkt for punkt hvordan man kan tegne fortegnslinja til en generell funksjon .
Hvordan tegner du fortegnslinja til en generell funksjon for ?
1. Finn alle løsningene (i det aktuelle intervallet) til likningen , altså Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0. Nullpunkt

2. Tegn inn en tall-linje, og marker følgende punkter på den:
- Nullpunktene til (disse fant du i punkt 1).
- Punktene der ikke er definert, altså de til funksjonen.kritiske punktene
Kritisk punkt
De kritiske punktene til en funksjon for er
1. Punkter der .
2. Punkter der ikke er definert.
3. Endepunktene til intervallet, og .
- Eventuelle bruddpunkter på funksjoner.
- Endepunktene – hvis det er noen – til intervallet .
3. Finn ut hvilket fortegn har mellom punktene du har markert. Regn ut funksjonsverdien for en x-verdi i intervallet, og se hvilket fortegn den har.
4. Tegn fortegnslinja til rett under tall-linja ved å bruke disse symbolene:
- ______ der ,
- - - - - - der ,
- o der ,
- > og < for å vise at funksjonen er positiv/negativ helt til, men ikke inkludert, et punkt.
Del på Facebook